2025. 2. 27. 05:52ㆍ머신러닝, 딥러닝 개념/지도 학습

이번에는 머신러닝의 선사시대 역할을 맡고 있는 선형 회귀에 대해 포스팅해보려고 한다. 선형 회귀는 개론에서도 약간 다룬 바 있지만 여기서는 수식과 코드를 동반하여 더 심화적인 내용까지 다룬다.
① 단순 선형 회귀(Simple Linear Regression)
선형 회귀(Linear Regression)에서 독립 변수는 하나 또는 그 이상이 될 수 있으나, 그 중에서 독립 변수가 하나인 경우만을 특별히 '단순 선형 회귀'라고 부른다. 독립 변수가 두 개 이상인 선형 회귀는 다중 선형 회귀(Multiple Linear Regression)라고 한다.

혹시 개론을 안 읽고 여기로 왔다면 개론을 먼저 읽고 오길 바란다. 선형 회귀에 대한 가장 기본적인 설명은 여기서 다 했다.
https://one-plus-one-is-two.tistory.com/9
머신러닝 개론 : 머신러닝 알고리즘, 손실 함수, 최적화
① 머신러닝 알고리즘지도 학습(Supervised Learning) : 라벨(정답)이 있는 데이터를 입력으로 받아 학습하는 알고리즘. 대표적으로 회귀와 분류가 있다.비지도 학습(Unsupervised Learning) : 라벨이 없는 데
one-plus-one-is-two.tistory.com
선형 회귀는 주어진 데이터를 가장 잘 대표하는 직선을 찾아가는 과정이라고 개론에서 언급한 바 있다.
그리고 오차 함수로는 주로 평균 제곱 오차(Mean Squared Error, MSE)를 사용한다는 것도 개론에서 언급했다.
최적화는 개론에서 언급한 것처럼 경사 하강법(Gradient Descent)을 사용할 것이다. 물론 다른 최적화 알고리즘을 사용해도 되지만 경사 하강법이 가장 설명하기 쉽고 이해하기도 쉬운 알고리즘이기 때문에 경사 하강법을 사용한다.
(1) 문제 제시
다음과 같은 데이터가 주어져 있다고 하자.

이를 그래프에 나타내보면 다음과 같다.

우리는 이 7개의 점들을 가장 잘 대표하는 직선을 찾을 것이다. 일단 직관적으로 우상향하는 직선이 나올 것으로 예상할 수 있지만, 오차를 최소화하는 가중치(
(2) 손실 함수
개론에서 MSE를 계산하는 식은 다음과 같다고 언급한 바 있다.

따라서 이 문제에서 선형 회귀식

여기서 MSE가 최소가 되도록 하는
일단 편의상 초깃값을

y값의 범위가 기껏해야 2.8 ~ 7.1인데 MSE가 27.73이면 너무 크다. 근데 크게 나오는게 당연하다.
(3) 최적화
최적화 알고리즘인 경사 하강법을 이용하여 적절한
경사 하강법에 대해 간단히 리뷰하면, 어떤 파라미터에 대한 손실 함수 기울기 값이 양수이면 파라미터 값을 줄이고, 기울기 값이 음수이면 파라미터 값을 늘리는 기법이었다. 따라서 우리는 MSE 함수의 기울기 값을 구하기 위해 MSE를 미분해야 한다.

여기서
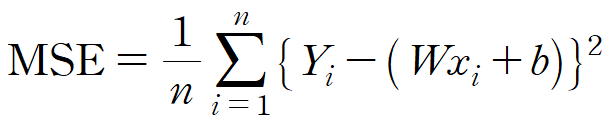
이 식에서 독립 변수는 총 4개(
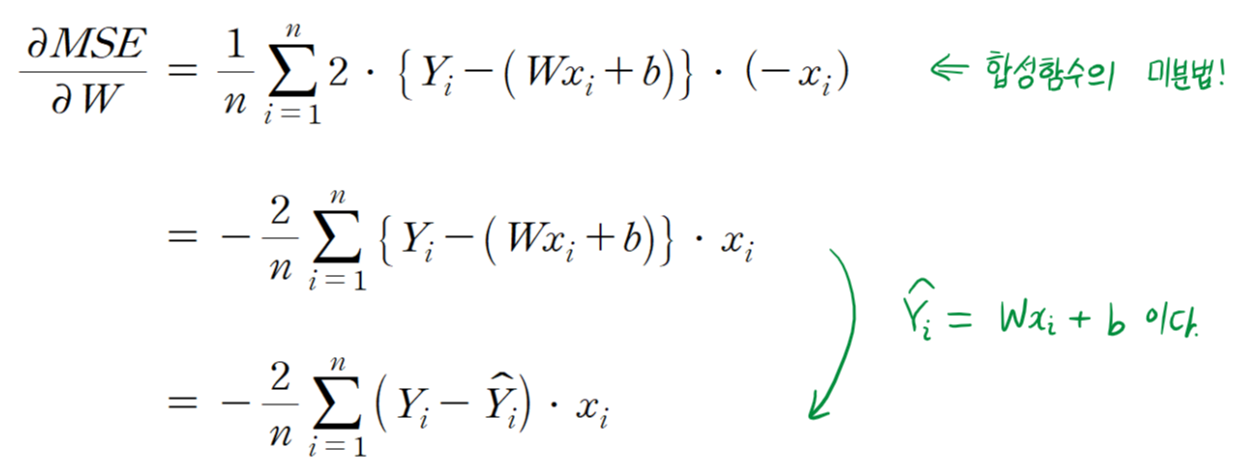
수식이 나와서 기겁할 수도 있지만 기껏해야 고등학교에서 배운 합성함수 미분법이다. 여러분이 대학생이라면 당연히 이 정도는 미분할 수 있어야 한다.
다음은 편향

지금까지 다음 두 식을 얻었다.
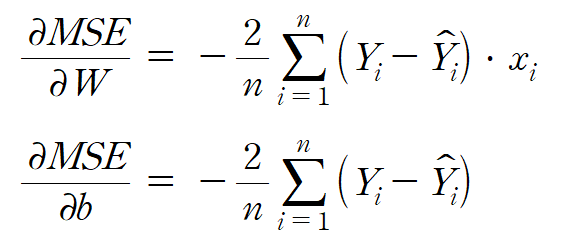
그러면 이제 실제 값을 대입해서 각각의 편미분 값을 구할 수 있다.
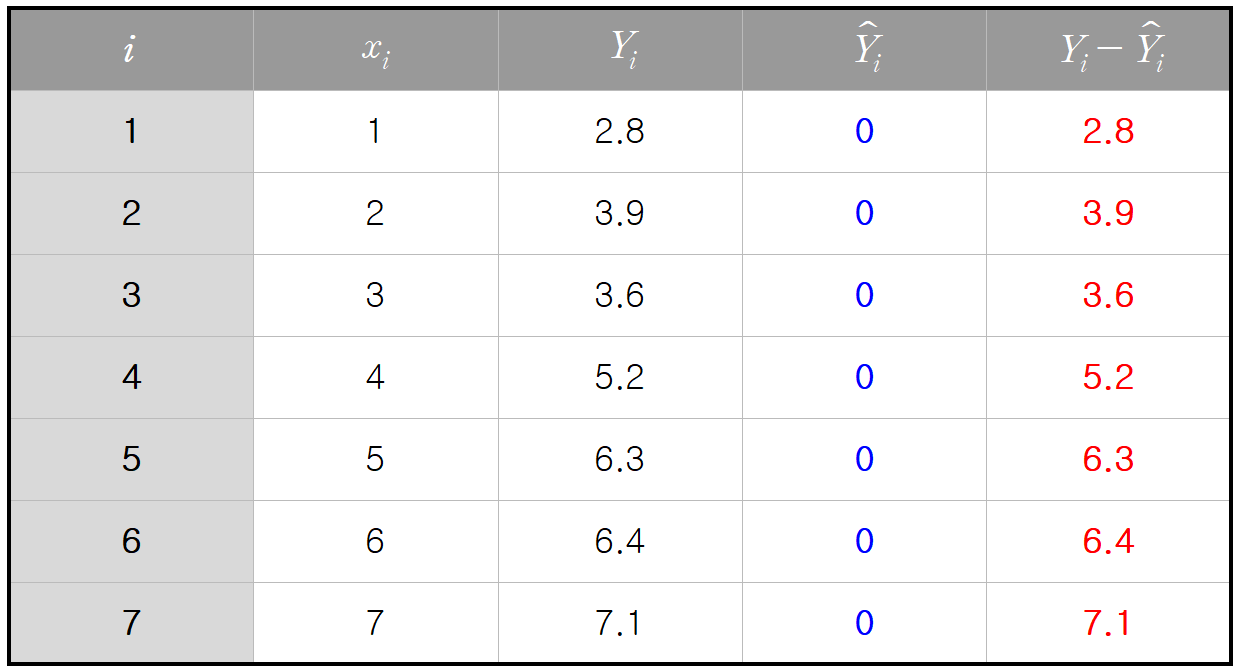
초깃값을
이를 토대로 MSE의

기울기가 모두 음수가 나왔으므로, 가중치
근데 여기서 의문점이 있다. 값을 키우긴 키우는데 얼마나 키워야 할까?

앞에서 구한 기울기에 적당한 양수
그러면 여기서 학습률을 어떻게 지정해주면 될까? 학습률을 높게 설정하면 빠른 학습이 가능하지만, 어느 정도 이상을 넘어가면 빠르게 학습되지도 않고 심지어는 최솟값을 찾지 못하고 발산할 수도 있다. 학습률을 낮게 설정하면 안정적으로 학습할 수 있으나 학습 속도가 매우 느려질 수 있으므로 적당한 학습률을 찾는게 중요하다.
학습률은 보통 0.001 ~ 0.1 범위에서 많이 쓰긴 한다. 나는 학습률을 0.01로 설정하고 계산을 수행했다.

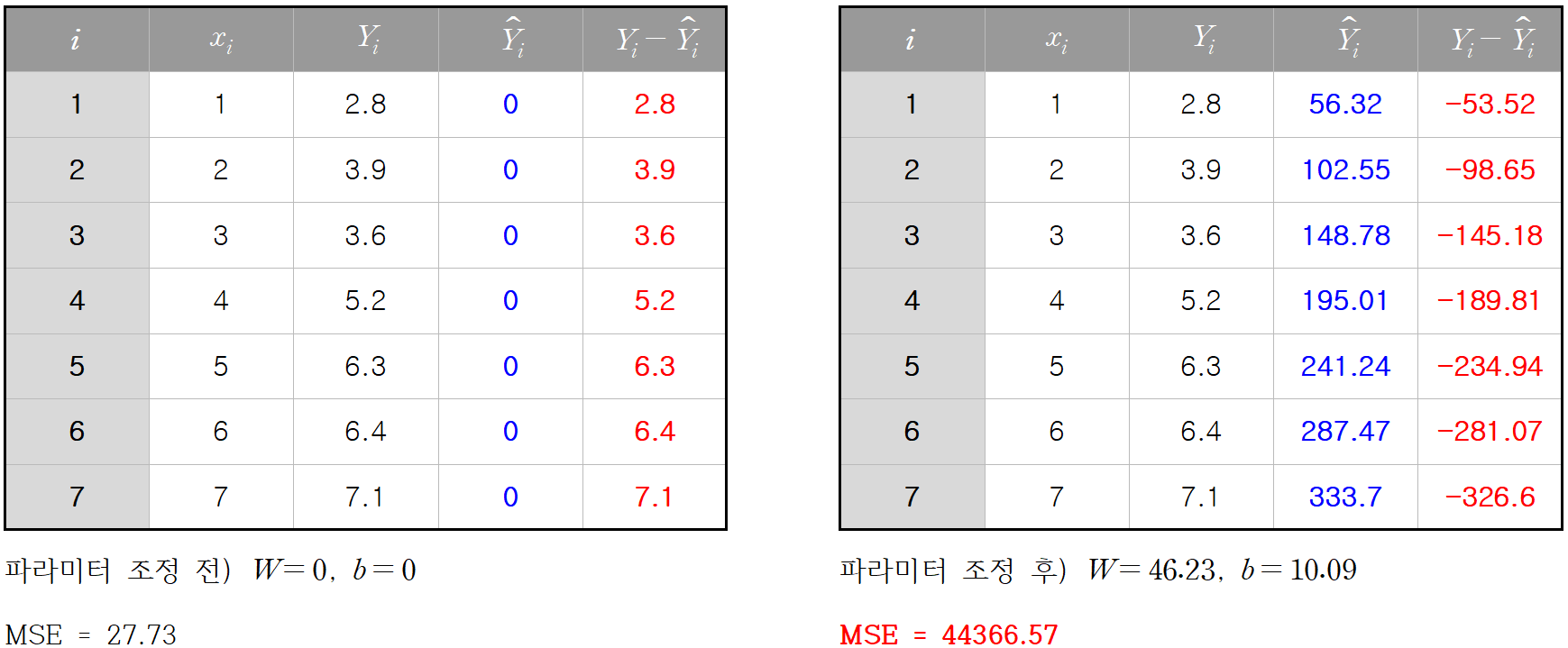
새로 갱신된 가중치는 0.4623, 새로 갱신된 편향은 0.1009이므로
그러면 새로운 선형 회귀 식으로 예측을 다시 수행해보겠다.

오른쪽이 새로 갱신한 선형 회귀식으로 예측한 결과이다. 빨간색으로 표시된 오차가 한 눈에 봐도 줄었음을 알 수 있다. MSE도 27.73에서 10으로 꽤 많이 줄었음을 알 수 있다.
여기서 끝나는게 아니라, 여기서 산출된 예측값을 토대로 또 다시 기울기를 구한 후 이를 이용해 파라미터를 조정해주는 작업을 이론상 무한히 반복하면 오차가 최소가 되는 지점에 도달할 수 있다. 근데 당연히 무한히 반복하는건 불가능하고, 학습 횟수는 적당히 많게 설정해주면 된다. 아 참고로 머신러닝에서는 학습 횟수를 에포크(epoch)라고 한다. 어차피 내가 여기서 언급 안해도 밥 먹고 화장실 가는것보다 더 자주 나오는 용어긴 하다...
(4) 학습률의 중요성?
1. 학습률을 너무 크게 설정했을 때
자 그러면 학습률의 중요성을 짧게라도 몸소 체험해보는 시간을 가져보자. 아까 만약에 학습률이 0.01이 아니라 1로 설정했으면 어땠을까?
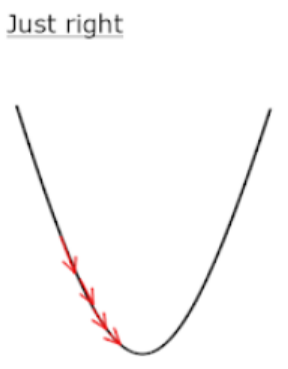
개선되기는 커녕 오히려 훨씬 악화되었다. MSE가 무려 만 단위를 넘어갈 정도로 심하게 악화되었다. 여기서 학습을 한 번 더 시키면 개선될까? 이거는 절대 개선되지 않고 오차가 무한대로 뻗어나갈 수밖에 없다. 한 마디로 학습률을 너무 크게 설정하면 학습이 영원히 안 되는 상황이 발생할 수도 있다. 이 상황을 그림으로 나타내면 다음과 같다.

2. 학습률을 너무 작게 설정했을 때
'아, 그러면 난 안정적인 학습을 위해 학습률을 0.00001로 잡겠어요!' 하면 어떻게 될까?

물론 학습률을 낮게 하면 안정적으로 성능이 개선되는건 사실이나, 너무 작게 잡으면 속 터지게 느려진다. 위 결과를 보면 27.73에서 27.70으로 고작 0.03 개선됐다. 게다가 또 알아야 하는 사실이, MSE가 작아질수록 기울기의 크기는 작아진다는 것을 알아야 한다. 점점 작아지는 기울기에 0.00001 같은 쥐똥같은 숫자나 계속 곱하고 있으면 차라리 강원도에 있는 우리 거북이가 부산까지 기어가는게 더 빠를 것 같을 정도의 속도를 보게 될 것이다. 이를 그림으로 표현하면 다음과 같다.

따라서 우리는 다음 그림처럼 효율적인 학습이 이루어질 수 있도록 적당한 학습률을 정해주는 것이 중요하다.
(5) 코드 작성하기
① 별도의 머신러닝 라이브러리 없이 구현
선형 회귀, MSE, 경사 하강법 조합의 학습은 그 방법이 매우 단순해서 사이킷런, 파이토치, 텐서플로우 등의 라이브러리를 사용하지 않고도 쉽게 구현할 수 있다. 물론 라이브러리를 갖다 쓰는게 가장 편한 방법이긴 하지만 선형 회귀는 구현 난이도가 어렵지 않고, 직접 구현해보면 머신러닝의 작동 원리를 이해하는데 도움이 되기 때문에 선형 회귀는 한 번 쯤은 직접 구현해보는 것이 좋은 것 같다. 특히 ㄱㅌㅎ 교수님 기계학습심화 듣는 사람들 이거 잘 봐라 실습 과제로 나오니까
먼저 다음 데이터를 NumPy 배열을 이용하여 다음 데이터를 코드로 옮긴다.

코드로 옮긴 결과는 다음과 같다.
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
이 데이터를 그래프에 시각화해보자.
import matplotlib.pyplot as plt
plt.scatter(x, y)
plt.show()
plt.scatter()는 산점도를 생성하는 함수인데, 파라미터가 꽤 많지만 여기서는 필수로 전달해야 하는 파라미터만 전달했다. x와 y를 리스트나 배열로 전달하면 모든 인덱스 i에 대해 점 (x[i], y[i])가 그래프에 찍히게 된다.
plt.show()로 그래프를 출력한 결과는 다음과 같다.

다음으로 MSE 구하는 코드를 구현해보자. MSE를 구하는 공식은 다음과 같다고 했다.

여기서
n = len(x) # 데이터의 개수
W = 0 # 가중치
b = 0 # 편향
y_pred = W*x + b
MSE = np.sum((y - y_pred) ** 2) / n
print("초기 MSE:", MSE)
내가 언급한 내용을 토씨 하나 안 틀리고 그대로 코드로 옮긴 것이다.
y_pred = W*x + b라고 하면 x에 [1, 2, 3, 4, 5, 6, 7]이 저장되어 있으니, y_pred에는 [W*1+b, W*2+b, …, W*7+b]이 저장된다. 만약에 파이썬에서 기본으로 제공되는 리스트를 사용했다면 map 함수를 이용해서 매칭하든가 했어야 할 것이다. 이처럼 넘파이 배열은 일반 리스트에 비해 더 직관적이고 편리한 연산을 제공한다. 따라서 머신러닝을 공부한다면 넘파이 배열의 사용에 익숙해지는 것이 중요하다.
같은 방식으로 MSE를 구하는 수식도 직관적으로 옮길 수 있다. (y - y_pred) ** 2라고 써놓기만 하면
[(y[0] - y_pred[0])**2, (y[1] - y_pred[1])**2, …, (y[6] - y_pred[6])**2]
와 같은 넘파이 배열이 생성되고, 이를 np.sum()에 전달하면 배열 내 모든 요소의 합이 반환된다. 즉, 다음과 같은 부분의 값을 손쉽게 구한 것이다.

이 값을 데이터의 개수 n으로 나누면 MSE가 구해지는 것이다. 위 코드의 출력 결과는 다음과 같다.
초기 MSE: 27.729999999999997
내가 직접 계산해서 구한 27.73과 똑같이 나왔음을 알 수 있다(27.72999…7로 나온 이유는 부동소수점 오차 때문이다).
다음으로 기울기값도 구현해보자. 기울기를 구하는 식도 내가 위에서 다 써놓은 바 있다.
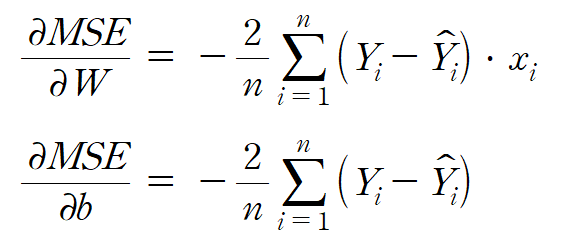
이를 그대로 코드로 옮겨놓기만 하면 된다.
diff_W = -2/n * np.sum((y - y_pred)*x)
diff_b = -2/n * np.sum((y - y_pred))
print("가중치(W)에 대한 기울기:", diff_W)
print("편향(b)에 대한 기울기:", diff_b)
출력 결과
가중치(W)에 대한 기울기: -46.22857142857143
편향(b)에 대한 기울기: -10.085714285714287
마지막으로 경사 하강법을 코드로 구현해보자. 경사 하강법으로 파라미터 값을 조정하는 것은 다음 수식을 따른다고 했다.

이것도 다음과 같이 코드로 그대로 옮겨 놓을 수 있다. 학습률
alpha = 0.01 # 학습률
W = W - alpha*diff_W
b = b - alpha*diff_b
print("학습 후 가중치(W)의 값:", W)
print("학습 후 편향(b)의 값:", b)
출력 결과
학습 후 가중치(W)의 값: 0.4622857142857143
학습 후 편향(b)의 값: 0.10085714285714287
이로써 가중치와 편향이 갱신되었다. MSE가 과연 얼마나 개선되었을지 출력해보자. 이전에 작성했던 y_pred와 MSE 구하는 코드를 그대로 복사해와서 실행시키면 된다.
y_pred = W*x + b
MSE = np.sum((y - y_pred) ** 2) / n
print("학습 후 MSE:", MSE)
출력 결과
학습 후 MSE: 9.999307836734692
MSE가 27.73에서 10으로 개선되었음을 확인할 수 있다. 하지만 이렇게 한 번만 학습시키고 끝내서는 안 된다. 실제로는 MSE를 10보다도 훨씬 더 많이 개선시킬 수 있다. 다음은 반복문을 이용해서 학습을 반복하는 코드이다.
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
n = len(x) # 데이터의 개수
W = 0 # 가중치
b = 0 # 편향
alpha = 0.01
y_pred = W*x + b
MSE = np.sum((y - y_pred) ** 2) / n
print(f"초기 MSE: {MSE:.3f}")
epochs = 1000
for epoch in range(epochs):
diff_W = -2/n * np.sum((y - y_pred)*x)
diff_b = -2/n * np.sum((y - y_pred))
W = W - alpha*diff_W
b = b - alpha*diff_b
y_pred = W*x + b
MSE = np.sum((y - y_pred) ** 2) / n
if (i+1) % 100 == 0:
print(f"epoch#{epoch+1}: W={W:.3f}, b={b:.3f}, MSE={MSE:.3f}")
에포크(반복횟수)를 1,000으로 줬는데, 실제 프로젝트를 할 때는 에포크 한 번 돌리는데도 꽤나 오래 걸리기 때문에 에포크를 1,000씩이나 주는 경우는 없다고 보면 된다. 하지만 이 반복문 안에는 시간이 오래 걸리는 코드가 전혀 없고 단순한 계산 코드만을 포함하기 때문에 에포크를 1,000으로 줘도 0.1초 안에 모든 작업이 끝난다.
출력 결과
초기 MSE: 27.730
epoch#100: W=0.993, b=0.824, MSE=0.460
epoch#200: W=0.911, b=1.232, MSE=0.285
epoch#300: W=0.855, b=1.510, MSE=0.204
epoch#400: W=0.817, b=1.698, MSE=0.167
epoch#500: W=0.791, b=1.827, MSE=0.149
epoch#600: W=0.773, b=1.914, MSE=0.141
epoch#700: W=0.761, b=1.974, MSE=0.138
epoch#800: W=0.753, b=2.014, MSE=0.136
epoch#900: W=0.748, b=2.041, MSE=0.135
epoch#1000: W=0.744, b=2.060, MSE=0.135
학습을 많이 반복했더니 MSE가 획기적으로 줄어드는 것을 확인할 수 있다. 초기 27.73에서 0.135까지 줄였다. 하지만 결과를 보면 알겠지만 MSE가 줄어드는 속도는 점점 느려지는 것을 알 수 있다. 제시된 7개의 점을 모두 지나는 직선은 존재하지 않기 때문에, MSE가 개선되는 것은 한계가 있다. 내가 직접 실험해보니 0.134가 한계치인듯 하다.
그러면 이제 적합시킨 결과를 그래프에 시각화해보자.
import matplotlib.pyplot as plt
line_x = np.array([1, 7])
line_y = W*line_x + b
plt.scatter(x, y, color="red", label="actual")
plt.plot(line_x, line_y, label="predicted")
plt.legend() # 레이블 표시
plt.show()
plt.plot() 함수를 이용하면 선분을 시각화할 수 있다. line_x에는 [1, 7]이 저장되어 있고 line_y에는 [W*1+b, W*7+b]가 저장되어 있으므로 여기서는 두 점
그래프 출력 결과는 다음과 같다.

직선이 주어진 데이터들에 대해 꽤 잘 적합되었음을 확인할 수 있다.
이왕 하는거 학습률의 중요성도 다시 살펴보자.
내가 직접 실험해보니 학습률을 0.046으로 올리는 것까지는 성능 개선의 효과가 분명히 있었다.
초기 MSE: 27.73
epoch#100: W=0.799, b=1.785, MSE=0.154
epoch#200: W=0.746, b=2.047, MSE=0.135
epoch#300: W=0.738, b=2.091, MSE=0.135
epoch#400: W=0.736, b=2.099, MSE=0.134
epoch#500: W=0.736, b=2.1, MSE=0.134
학습률을 0.01로 할 때는 에포크를 800번 넘게 돌려야 MSE가 0.135까지 개선됐는데, 학습률을 0.046으로 할 때는 200번 이하의 에포크로 같은 성능을 낼 수 있다. 하지만 학습률을 0.047, 0.048로 늘리면 학습률을 0.046으로 할 때보다 학습 속도가 오히려 느려지고, 0.049부터는 아예 발산해버린다. 다음은 학습률을 0.049로 했을 때 출력 결과이다.
초기 MSE: 27.73
epoch#100: W=-51.124, b=-8.664, MSE=58369.264
epoch#200: W=-2417.934, b=-486.372, MSE=126689540.543
epoch#300: W=-112681.899, b=-22753.152, MSE=274978299589.134
epoch#400: W=-5249715.499, b=-1060130.931, MSE=596837473729007.9
epoch#500: W=-244576462.05, b=-49390017.287, MSE=1.2954293868994194e+18
MSE가 한계를 모르고 치솟는 것을 확인할 수 있다. 이렇듯 학습률을 너무 크게 주면 성능이 오히려 악화되는 문제가 발생할 수 있다.
학습률을 너무 작게 준 상황도 확인해보자. 다음은 학습률을 0.00001로 줬을 때 출력 결과이다.초기 MSE: 27.730
epoch#1000: W=0.378, b=0.084, MSE=12.530
epoch#2000: W=0.627, b=0.142, MSE=5.915
epoch#3000: W=0.790, b=0.182, MSE=3.035
epoch#4000: W=0.898, b=0.211, MSE=1.779
epoch#5000: W=0.968, b=0.233, MSE=1.230
epoch#6000: W=1.014, b=0.249, MSE=0.988
epoch#7000: W=1.044, b=0.263, MSE=0.880
epoch#8000: W=1.063, b=0.274, MSE=0.830
epoch#9000: W=1.075, b=0.283, MSE=0.806
epoch#10000: W=1.083, b=0.292, MSE=0.792
에포크를 1,000이 아니라 10,000으로 줬는데도 성능이 최대로 개선되지 않았다. 실제로 MSE를 0.134까지 줄이기 위해서는 1분이 넘는 시간이 소요된다. 물론 학습률을 너무 크게 줬을 때와 달리 이건 학습이 되고 있기는 하니까 상황이 더 낫다고 볼 수는 있다. 하지만 실제 머신러닝 프로젝트할 때는 에포크를 한 번 돌리는 것도 오래 걸리기 때문에, 이렇게 학습률을 지나치게 작게 설정하면 하룻밤 자고 일어나도 학습이 안 끝나 있는 수가 있다. 따라서 적절한 학습률 설정이 중요하다는 것을 재차 강조한다.
② NumPy로 수행하기
사실 NumPy는 그 자체로는 머신러닝 라이브러리가 아니긴 하다. 위키피디아에 따르면 NumPy 는 행렬이나 일반적으로 대규모 다차원 배열을 쉽게 처리할 수 있도록 지원하는 파이썬의 라이브러리로, 머신러닝을 위한 도구 정도로 쓰이는거지 머신러닝을 수행하는 라이브러리는 아니다. 하지만 선형 회귀는 사실 MSE를 최소화시키는 가중치와 편향 값은 정해져 있다(뒤에서 언급). 따라서 위에서 언급한 방법처럼 굳이 모델을 학습시키는 식으로 최적값을 찾지 않아도 되는데, 그래서 그런지 선형 회귀를 수행하는 기능을 NumPy에서도 제공한다.
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
W, b = np.polyfit(x, y, 1)
y_pred = W*x + b
MSE = np.sum((y - y_pred) ** 2) / n
print(f"W = {W}")
print(f"b = {b}")
print(f"MSE = {MSE}")
np.polyfit() 함수를 이용하면 다항 회귀를 수행할 수 있다. 첫 번째 인자와 두 번째 인자에 각각 x와 y에 해당하는 배열을 전달하고, 세 번째 인자는 몇차함수로 적합시킬지를 정하는건데 직선은 일차함수이므로 세 번째 인자는 1을 전달하면 된다.
출력 결과는 다음과 같다.
W = 0.7357142857142857
b = 2.1
MSE = 0.13448979591836732
MSE가 최대 개선 한계치인 0.134로 나타났음을 확인할 수 있다.
③ SciPy로 수행하기
SciPy는 파이썬의 과학 및 수학 계산을 위한 오픈 소스 라이브러리이다. 이를 이용하여 선형 회귀를 진행하면 여러 통계적인 수치가 많이 나온다.
from scipy import stats
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
result = stats.linregress(x, y)
print(result)
scipy 라이브러리의 stats.linregress() 함수를 통해 선형 회귀를 수행할 수 있다. 다음은 result의 출력 결과이다.
LinregressResult(slope=0.7357142857142858, intercept=2.1000000000000005, rvalue=0.9703173691875804, pvalue=0.0002869252163705624, stderr=0.08200298650609213, intercept_stderr=0.36672850437123994)
결과가 객체에 담겨져 출력된다. slope는 기울기, intercept는 절편, rvalue는 상관계수, pvalue는 p값(통계학에서 배웠는데 까먹었다), stderr는 표준 오차, intercept_stderr는 절편에서의 표준 오차라고 한다. 통계학도 시간 되면 공부해야겠다(공부할게 왜 이렇게 많냐).
④ scikit-learn으로 수행하기
위의 NumPy와 SciPy는 머신러닝 라이브러리는 아니고 머신러닝을 할 때 함께 사용하는 도구 라이브러리 정도였는데, 여기부터는 본격적으로 머신러닝 라이브러리를 다룬다. scikit-learn(사이킷런이라고 읽음)과 뒤에 나오는 TensorFlow, Keras, PyTorch 모두 머신러닝 라이브러리이다.
사이킷런은 사용하기 쉬우며, 강력하고 다양한 머신러닝 알고리즘들을 제공하지만 딥러닝이나 강화 학습을 수행할 수 없다는 단점이 있다. 여기서 scikit-learn, TensorFlow, Kears, PyTorch라는 총 4개의 머신러닝 라이브러리를 사용할건데, 실제로 사이킷런으로 구현한 코드가 이 중에서 압도적으로 직관적이고 쉽다. 안타깝게도 뒤에 나오는 코드들은 난이도가 좀 있어서 아직 초보자라면 사이킷런으로 구현한 코드만 보고 넘어가도 좋을 것 같다. 사이킷런으로 선형 회귀를 구현한 코드는 다음과 같다.
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
reg = LinearRegression() # 선형 회귀 클래스 객체 저장
reg.fit(x.reshape(-1, 1), y) # 인자로 x와 y 전달
W, b = reg.coef_, reg.intercept_ # coef_(계수), intercept_(절편)
y_pred = W*x + b
MSE = mean_squared_error(y, y_pred)
print(f"W = {W}")
print(f"b = {b}")
print(f"MSE = {MSE}")
선형 회귀에는 다양한 머신러닝 모델과 성능 지표를 제공하기 때문에, 필요한 것을 import 해와서 그대로 사용하면 된다.
reg.fit()를 호출하여 선형 회귀 피팅을 진행할 때 x에 reshape(-1, 1)을 적용한게 눈에 띄는데, 이게 무슨 의미일까?
x는 원래 크기가 (7,)인 1차원 데이터이다. 하지만 사이킷런에서 선형 회귀를 수행할 때 첫 번째 인자에 2차원 데이터가 오기를 요구한다. 따라서 x에 reshape(-1, 1)을 적용하여 x를 2차원 데이터로 만들어주는 것이다.
두 번째 인자가 1이므로 열은 1로 맞추는데, 첫 번째 인자를 -1로 한 것은 행은 나머지 요소의 크기에 따라 자동으로 맞추겠다는 뜻이다. 즉, x에 들어있는 데이터의 개수가 총 7이고 열의 크기는 1로 하기로 했으므로 행의 개수는 자동으로 7이 된다. 따라서 x.reshape(-1, 1)의 차원 변환 결과는 (7, 1), 즉 7×1 크기의 행렬이 된다.
행의 개수는 데이터의 개수를 의미하며, 열의 개수는 가중치의 개수를 의미한다고 생각하면 된다. 이건 단순 회귀 분석이라 가중치가 하나이므로 열의 개수를 1로 설정하는데, 다중 회귀 분석이라면 열의 개수가 2 이상이 될 수 있다.
선형 회귀를 수행했다면 .coef_로 가중치(계수)를 꺼내올 수 있고, .intercept_로 편향(절편)을 꺼내올 수 있다. 이때, 편향은 실수로 반환되지만 가중치는 배열에 담겨져 반환된다. 물론 단순 선형 회귀만 다룬다면 가중치가 어차피 1개이니 배열에 담을 필요가 없겠지만, 사이킷런의 LinearRegression 객체는 다중 선형 회귀도 다루기 때문에 가중치가 여러 개일 것을 대비해서 가중치를 배열에 담아서 반환한다.
또한 sklearn.metrics에서 mean_squared_error를 import 해오면 내가 직접 MSE 공식을 쓰지 않고도 편리하게 MSE를 계산할 수 있다. 공식 문서를 보면 첫 번째 인자에 참값을 전달하고 두 번째 인자에 예측값을 전달하라고 되어있는데, MSE 특성상 둘이 바꿔서 전달해도 결과는 똑같이 나올 것 같다.
위 코드를 실제로 실행시켜보면 결과는 다음과 같다.
W = [0.73571429]
b = 2.100000000000001
MSE = 0.13448979591836724
이쯤되면 눈치 챘을 것이다. NumPy, SciPy, scikit-learn 모두 아무런 학습 과정 없이 같은 값을 반환하고 있다. NumPy에서도 살짝 귀띔을 해주긴 했지만 MSE를 최소화시키는
⑤ TensorFlow로 수행하기
TensorFlow는 PyTorch와 함께 가장 대표적으로 사용되는 머신러닝 라이브러리이다. 사실 필자도 각 라이브러리가 어떤 특징이 있는지 어떤 장단점이 있는지 잘 모르는데, 유명한 책 저자가 이를 잘 설명해준 글이 있어 글 링크를 공유하려고 한다.
딥러닝 프레임워크 비교(텐서플로 VS 케라스 VS 파이토치) : 표로 한눈에!
현재 소개된 딥러닝 프레임워크들은 각각 다른 목적으로 제작되었으며, 고유한 기능과 특성을 제공합니다. 이중 유명한 딥러닝 프레임워크 텐서플로, 케라스, 파이토치를 소개하고 표로 장단점
hongong.hanbit.co.kr
앞으로 프레임워크에 대한 설명은 위 글의 내용을 인용하려고 한다.
텐서플로는 구글이 개발한 오픈소스 소프트웨어 라이브러리이며 머신러닝과 딥러닝을 쉽게 사용할 수 있도록 다양한 기능을 제공한다. 텐서플로는 데이터 플로우 그래프(Data Flow Graph) 구조를 사용하는 특징이 있다. 이는 수학 계산식과 데이터의 흐름을 노드(Node)와 엣지(Edge)를 사용한 방향성 그래프로 표현하는 방식이다. 각 노드 사이의 연결이나 다차원 배열 등을 의미하는 텐서 사이의 연결 관계를 풍부하게 표현할 수 있으며, 텐서보드 시각화 도구 모음을 사용하면 웹 기반의 대화형 대시보드에서 그래프 실행 방법에 대한 검사나 프로파일링도 가능하다.
텐서플로는 주로 이미지 인식이나 반복 신경망 구성, 기계 번역, 필기 숫자 판별 등을 위한 각종 신경망 학습에 사용된다. 특히 대규모 예측 모델 구성에 뛰어나 테스트부터 실제 서비스까지 사실상 거의 모든 딥러닝 프로젝트에서 범용적으로 활용할 수 있다. 무엇보다 구글에서 전폭적으로 지원하고 있기 때문에 지속적인 성능 개선과 지원에서 타 프레임워크보다 빠르고 안정적이란 부분이 강점이다. 이 밖에도 추상화 수준이 높아 텐서플로를 활용하면 개발자는 알고리즘의 세세한 구현보다 전체적인 논리 자체에 더 집중할 수 있게 되며 확장성 또한 뛰어나다.
단점으로는 딥러닝 모델을 만드는 데 기초 레벨부터 직접 작업해야 하기 때문에 초보자가 사용하기 어려울 수 있다고 한다. 실제로 구현 코드를 보면 난이도가 꽤 어렵다는 것을 알 수 있다.
import tensorflow as tf
import numpy as np
# 1. 변수 초기화
x = np.array([1, 2, 3, 4, 5, 6, 7], dtype=np.float32)
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
# 2. 학습할 변수 (가중치와 편향)
W = tf.Variable(tf.random.normal([1, 1]), dtype=tf.float32) # 가중치 (1x1 행렬)
b = tf.Variable(tf.random.normal([1]), dtype=tf.float32) # 편향 (스칼라)
MSE = np.inf
# 3. 선형 회귀 모델 정의
def linear_regression(x):
return tf.matmul(x, W) + b # y = Wx + b
# 4. 손실 함수 (평균 제곱 오차, MSE)
def mse_loss(y_true, y_pred):
return tf.reduce_mean(tf.square(y_true - y_pred))
# 5. 옵티마이저 (경사 하강법)
optimizer = tf.keras.optimizers.SGD(learning_rate=0.01)
# 6. 학습 과정 (경사 하강법 적용)
epochs = 1000
for epoch in range(epochs):
with tf.GradientTape() as tape: # 자동 미분을 위한 GradientTape
y_pred = linear_regression(x.reshape(-1, 1)) # 모델 예측값
MSE = mse_loss(y.reshape(-1, 1), y_pred) # 손실 계산
# 기울기(gradient) 계산
gradients = tape.gradient(MSE, [W, b])
# 가중치와 편향 업데이트
optimizer.apply_gradients(zip(gradients, [W, b]))
# 100번마다 손실 출력
if (epoch + 1) % 100 == 0:
print(f"epoch#{epoch+1}: W={W.numpy()[0][0]:.3f}, b={b.numpy()[0]:.3f}, MSE={MSE:.3f}")
print("\n최종 결과")
print(f"W = {W.numpy()[0][0]}")
print(f"b = {b.numpy()[0]}")
print(f"MSE = {MSE}")
② ~ ④와 달리 W와 b를 바로 계산해서 출력하지 않고 학습을 통해 최적값을 찾아나가는 코드이다.
코드를 보면 선형 회귀는 linear_regression() 함수로, 손실 함수 MSE는 mse_loss() 함수로 구현하는 등 처음부터 깡구현하는 것을 볼 수 있다. 텐서플로우 자체에는 scikit-learn의 LinearRegression 같은 클래스나 mean_squared_error 같은 함수는 없다. 따라서 밑바닥부터 깡구현을 해야 한다는게 특징이다.
텐서플로우에서 제공하는 함수들에 대해서는 다음에 깊게 알아볼 기회가 있다면 알아보기로 하고, 여기서는 출력값만 제시하고 넘어가려고 한다.
epoch#100: W=1.190, b=-0.149, MSE=1.154
epoch#200: W=1.045, b=0.570, MSE=0.606
epoch#300: W=0.946, b=1.059, MSE=0.353
epoch#400: W=0.879, b=1.392, MSE=0.236
epoch#500: W=0.833, b=1.618, MSE=0.181
epoch#600: W=0.802, b=1.772, MSE=0.156
epoch#700: W=0.781, b=1.877, MSE=0.145
epoch#800: W=0.766, b=1.948, MSE=0.139
epoch#900: W=0.757, b=1.997, MSE=0.137
epoch#1000: W=0.750, b=2.030, MSE=0.135
최종 결과
W = 0.7498882412910461
b = 2.029811382293701
MSE = 0.13548311591148376
학습으로 가중치와 편향값을 찾아나가는 코드라 완벽하게 최적화시키지는 못했지만, 에포크를 늘리면 완벽한 값에 매우 근접하게 최적화시킬 수 있을 것이다. 아니면 학습률을 0.01에서 0.046으로 늘리면 훨씬 더 빠르게 학습시킬 수 있다.
⑥ Keras로 수행하기
케라스는 텐서플로우의 문제를 해결하기 위해 보다 단순화된 인터페이스를 제공하기 위해 개발되었다. 케라스의 핵심적인 데이터 구조는 모델이다. 케라스에서 제공하는 시퀀스 모델로 원하는 레이어를 쉽게 순차적으로 쌓을 수 있으며, 다중 출력 등 더 복잡한 모델을 구성할 때는 케라스 함수 API를 사용하여 쉽게 구성할 수 있다. 이처럼 케라스는 딥러닝 초급자도 각자 분야에서 손쉽게 딥러닝 모델을 개발하고 활용할 수 있도록 직관적인 API를 제공한다.
텐서플로우의 문제를 해결하기 위해 개발된만큼 사용하기 쉽고 직관적이다. 일반 사용 사례에 최적화된 간단하고 일관된 인터페이스를 제공하며, 사용자 오류에 대해 명확하고 실용적인 피드백을 제공한다고 한다. 또한 케라스의 구성 요소는 모듈 형태로, 각 모듈이 독립성을 갖기 때문에 새로운 모델을 만들 때 각 모듈을 조합해 쉽게 새로운 모델을 만들 수 있다.
모듈화의 한계로 복잡한 프로젝트에 구현 범위가 다소 좁은 편이라고 한다. 또한 케라스는 다양한 백엔드 위에서 동작하기 때문에 어떤 오류가 발생했을 때 케라스 자체의 문제인지, 백엔드 언어의 문제인지 특정하기 어려운 단점이 있다.
kears 라이브러리는 tensorflow 라이브러리 안에 있기 때문에, Keras API를 사용하려면 from tensorflow.kears.* import * 형식으로 임포트하면 된다.
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import MeanSquaredError
from tensorflow.keras.optimizers import SGD
import numpy as np
# 데이터 정의
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
# Keras 모델 정의 (Dense layer 1개)
model = Sequential([
Dense(1, input_shape=(1,))
])
# 모델 컴파일 (손실 함수: MSE, 옵티마이저: SGD)
model.compile(optimizer=SGD(learning_rate=0.01), loss='mse')
# 모델 학습
model.fit(x, y, epochs=1000, verbose=0) # verbose=0이면 출력 생략
# 최종 가중치와 편향 출력
W, b = model.layers[0].get_weights()
y_pred = model.predict(x)
MSE = MeanSquaredError()(y, y_pred).numpy()
print(f"W = {W[0]}")
print(f"b = {b[0]}")
print(f"MSE = {MSE}")
케라스 없이 텐서플로우로만 깡구현했을 때보다 코드가 훨씬 더 직관적이고 쉬워졌다. model을 정의한 부분에서 볼 수 있는 것처럼, 케라스는 시퀀스 모델을 정의하여 그 안에 원하는 계층(layer)을 순차적으로 쌓아올릴 수 있다. 이 코드에서는 Dense 계층 하나만을 넣어줬다. 사실 Dense 계층은 프로젝트 글인 Dogs vs. Cats (2)를 보면 무슨 용도로 사용하는 계층인지 구체적으로 알 수 있다. 하지만 여기서는 그냥 선형 회귀를 하기 위해 존재하는 것이라고 치자.
Dense(1, input_shape=(1,))에서 첫 번째 인자로 전달한 1은 출력값이 1개라는 뜻으로, 여기서는
그리고 여기서는 최적화 함수(옵티마이저, optimizer)를 경사 하강법이 아닌 확률적 경사 하강법(Stochastic Gradient Descent)을 사용했는데, 이는 다음에 옵티마이저를 주제로 한 글을 쓸 때 다루게 될 것이다.
모델을 컴파일하고 학습 시킨 후 model.layers[0].get_weights() 함수를 호출하면 [가중치, 편향] 형태로 파라미터 값을 받아낼 수 있다. 이를 W, b 변수에 각각 나눠서 받아낸다.
MSE는 MeanSquaredError 객체를 만든 후에 (실젯값, 예측값) 형태로 인자를 전달하면 MSE를 계산한 결과가 반환된다. 이때, 반환되는 자료형은 tf.Tensor인데 이를 numpy로 바꾸려면 뒤에 .numpy()를 붙여주면 된다.
코드를 실행한 결과는 다음과 같다.
W = [0.7440334]
b = 2.0588040351867676
MSE = 0.13482941687107086
⑦ PyTorch로 수행하기
선형 회귀를 7가지 방법으로 구현하는 미친 짓을 하는 사람이 나 말고 또 있을지 모르겠다.
토치(Torch)는 페이스북의 AI 연구 팀이 개발한 파이썬 기반 오픈소스 머신러닝 라이브러리다. 파이토치는 토치(Torch)라는 머신 러닝 라이브러리에 바탕을 두고 만들어졌다. 파이토치는 텐서플로와 다르게 절차가 간단하고 그래프가 동적으로 변화할 수 있으며 코드 자체도 파이썬과 유사해 진입 장벽이 낮은 편이다.
그래프를 만들면서 동시에 값을 할당하는 Define by run 방식으로 코드를 깔끔하고 직관적으로 작성할 수 있다는 것이다. 또한 학습 속도도 텐서플로보다 빠르다. 텐서플로가 유기적을 신경망을 만들 수 없어 성능의 한계를 가지고 있는 반면, 파이토치는 메모리에서 연산을 하면서도 신경망 사이즈를 최적으로 바꾸면서 동작시킬 수 있다. 파이토치는 Numpy를 대체하면서도 GPU를 이용한 연산이 가능하며 유연하고 빠르기 때문에 최근 딥러닝 관련 논문에서는 텐서플로보다 파이토치를 선호하는 추세이다.
import torch
from torch import nn
from torch import optim
x = torch.FloatTensor([1, 2, 3, 4, 5, 6, 7]).unsqueeze(-1)
y = torch.FloatTensor([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1]).unsqueeze(-1)
W, b, MSE = 0, 0, 0
model = nn.Linear(1, 1)
loss = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
epochs = 1000
for epoch in range(epochs):
output = model(x)
MSE = loss(output, y)
optimizer.zero_grad()
MSE.backward()
optimizer.step()
if (epoch + 1) % 100 == 0:
W, b = list(model.parameters())
print(f"epoch#{epoch+1}: W={float(W):.3f}, b={float(b):.3f}, MSE={MSE:.3f}")
print("\n최종 결과")
print(f"W = {float(W)}")
print(f"b = {float(b)}")
print(f"MSE = {MSE}")
여기에서는 넘파이 배열 대신에 파이토치에서 제공하는 텐서(Tensor)라는 객체를 사용한다. unsqueeze(-1)은 차원을 늘려주는 기능을 하는데, 사이킷런의 reshape와 비슷한 기능을 하는 메서드라고 생각하면 된다. unsqueeze의 인자로는 크기가 1인 차원을 어디에 추가할지를 전달하면 되는데, -1을 전달하는 것은 마지막에 추가하겠다는 뜻이므로 원래 크기가 (7,)인 1차원 텐서였던 x와 y는 모두 크기가 (7, 1)인 2차원 텐서가 된다.
optimizer.zero_grad()
MSE.backward()
optimizer.step()
이 세 줄의 코드에 대해 간단히 언급하자면
optimizer.zero_grad는 모든 기울기를 0으로 초기화하는 함수이고,
MSE.backward()는 역전파를 통해 기울기를 계산해오는 함수이며,
optimizer.step()은 계산된 기울기를 바탕으로 최적화를 수행하는 함수이다.
이 세 코드는 파이토치에서 밥 먹듯이 쓰이는 함수들이므로 파이토치를 공부한다면 앞으로 자주 보게 될 것이다.
실행 결과는 다음과 같았다.
epoch#100: W=0.942, b=1.080, MSE=0.344
epoch#200: W=0.876, b=1.406, MSE=0.231
epoch#300: W=0.831, b=1.628, MSE=0.179
epoch#400: W=0.801, b=1.779, MSE=0.155
epoch#500: W=0.780, b=1.882, MSE=0.144
epoch#600: W=0.766, b=1.951, MSE=0.139
epoch#700: W=0.756, b=1.999, MSE=0.137
epoch#800: W=0.750, b=2.031, MSE=0.135
epoch#900: W=0.745, b=2.053, MSE=0.135
epoch#1000: W=0.742, b=2.068, MSE=0.135
최종 결과
W = 0.7421406507492065
b = 2.068176746368408
MSE = 0.13469399511814117
(6) 최소제곱법
최소제곱법, 또는 최소자승법, 최소제곱근사법, 최소자승근사법(method of least squares, least squares approximation)은 어떤 계의 해방정식을 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합(SS)이 최소가 되는 해를 구하는 방법이다.
지금까지 선형 회귀 모델을 학습시키는 방법을 구구절절 설명했지만 사실 단순 선형 회귀에서 MSE를 최소화시키는 것은 최소제곱법으로 공식화할 수 있어서, 거기에 값만 대입해주면 MSE가 최소가 되는
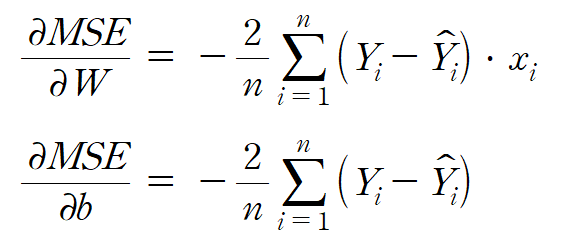
우리는 이 두 값이 모두 0이 되어야 MSE가 최소가 된다는 것을 알고 있다. 이를 동시에 0으로 만드는 것을 공식화 해볼 수 있을 것 같다. 먼저

편의상 시그마 아래 i=1과 시그마 위 n은 생략하기로 한다. 다음은
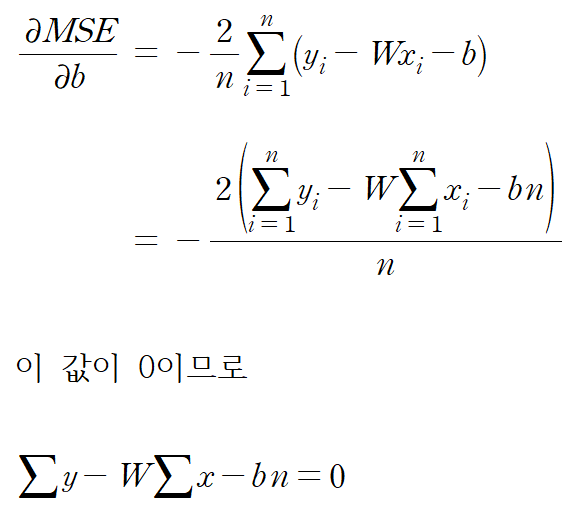
지금까지 유도한 두 방정식을 다음과 같이 연립해서 풀어주면 된다(이항은 미리 해놓았다).


위에서 아래를 빼주면

좌변에 W만 남도록 중괄호 안의 식을 양변에 나누면

여기까지만 해도 훌륭하지만 조금만 더 간단하게 만들어 보자. 먼저 분자를 간단히 하는 과정은 다음과 같다.

여기서
분자를 유도했으면 분모는 훨씬 쉽게 유도할 수 있다. 분자에서
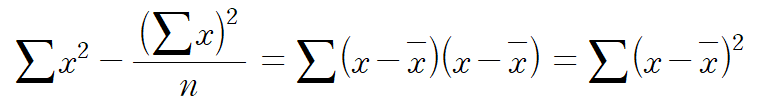
따라서 MSE를 최소화시키는

다음으로 MSE가 최소가 되도록 하는

이전에 이 수식을 얻은 적이 있었다.
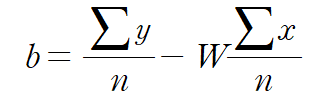
그런데 앞에서

따라서 가중치와 편향을 다음과 같이 설정하면, MSE가 반드시 최소가 된다.
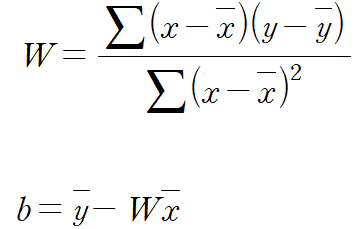
정말 그런지 파이썬 코드로 확인해보자.
from sklearn.metrics import mean_squared_error
import numpy as np
x = np.array([1, 2, 3, 4, 5, 6, 7])
y = np.array([2.8, 3.9, 3.6, 5.2, 6.3, 6.4, 7.1])
n = len(x) # 데이터의 개수
bar_x = np.mean(x) # x의 평균
bar_y = np.mean(y) # y의 평균
W = (np.sum((x - bar_x)*(y - bar_y) / np.sum((x - bar_x)**2)))
b = bar_y - W * bar_x
print(f"W = {W}")
print(f"b = {b}")
y_pred = W*x + b
MSE = mean_squared_error(y_pred, y)
print(f"MSE = {MSE}")
출력 결과
W = 0.7357142857142857
b = 2.100000000000001
MSE = 0.13448979591836724
모델을 학습시키지 않고 한 방에 최적값을 얻은 것을 확인할 수 있다.
사실 여기서 다중 선형 회귀까지 다루려고 했는데, 단순 선형 회귀도 깊게 파니까 내용이 많다. 따라서 다중 선형 회귀는 다음으로 넘기려고 한다.
'머신러닝, 딥러닝 개념 > 지도 학습' 카테고리의 다른 글
| 지도 학습(6) : 서포트 벡터 머신 (1) | 2025.03.14 |
|---|---|
| 지도 학습(5) : k-최근접 이웃 (4) | 2025.03.10 |
| 지도 학습(4) : 로지스틱 회귀 (3) | 2025.03.10 |
| 지도 학습(3) : 다항 회귀, 릿지 회귀, 라쏘 회귀, 엘라스틱 넷 (1) | 2025.03.05 |
| 지도 학습(2) : 다중 선형 회귀 (1) | 2025.03.01 |