지도 학습(3) : 다항 회귀, 릿지 회귀, 라쏘 회귀, 엘라스틱 넷

 

① 다항 회귀(Polynomial Regression)

다항 회귀는 주어진 데이터를 다음과 같이 다항함수 꼴로 적합시키는 회귀이다.

이번 내용은 앞에서 포스팅한 다중 선형 회귀에 대해 알고 있어야 이해하기가 쉽다. 따라서 아직 해당 내용을 읽지 않았다면 읽고 오는 것을 권장한다.

https://one-plus-one-is-two.tistory.com/12

지도 학습(2) : 다중 선형 회귀

 

 

다항 회귀도 다중 선형 회귀와 비슷하게 다음과 같이 벡터를 사용하여 나타낼 수 있다. 

 

이때 내가 처음에 제시한 식에서 $w_0$이 편향 $b$에 해당한다.

이렇게 놓고 보면, 다항 회귀의 벡터식과 다중 선형 회귀의 벡터식은 상당히 유사하다.

 

얼핏 보면 틀린 그림 찾기인줄 알 정도로 차이가 거의 안 나 보이는데, 차이가 있다면 다중 선형 회귀는 $x$에 붙는 숫자가 오른쪽 아래(아래 첨자)이고 다항 회귀는 $x$에 붙는 숫자가 오른쪽 위(지수)라는 점이다.

 

그렇다면 다항 회귀를 $x_1=x^1$, $x_2=x^2$, $\cdots$인 다중 선형 회귀로 생각해도 전혀 문제가 되지 않을 것 같다. 

 

예를 들어, 다음과 같은 데이터가 주어져 있다고 하자.

 

이를 이차식 $y=w_0+w_{1}x+w_2{x}^2$으로 적합시킨다고 하자. 그렇다면 사실 이 문제는 다음과 같이 주어진 데이터에 대해 다중 선형 회귀를 하라는 것과 다름이 없다.

 

따라서 이 이상의 진행 과정을 언급하는 것은 앞에서 포스팅한 다중 선형 회귀의 내용과 상당 부분이 중복된다. 그러므로 바로 코드로 구현해보도록 하자.

 

(1) 코드 실습

① 별도의 머신러닝 라이브러리 없이 구현

우선 이차 다항 회귀를 적용할만한 데이터를 임의로 생성해보자.

import numpy as np
import matplotlib.pyplot as plt

n = 150
x = np.linspace(1, 5, n)  # 양 끝점 포함하여 일정한 간격으로 n개의 수 반환
noise = np.random.rand(n) - 0.5  # [-0.5, 0.5] 범위의 노이즈 n개 생성
y = x**2 - 6*x + 10 + noise

plt.scatter(x, y)
plt.show()

 

np.linspace() 함수는 양 끝점을 포함하여 그 사이의 수를 일정한 간격으로 n개를 추출해 넘파이 배열로 반환하는 함수이다. 예를 들어, np.linspace(1, 5, 3)이라면 1과 5를 포함하여 이 사이의 수를 3개 반환하므로 [1. 3. 5.]라는 배열이 반환되고, np.linspace(1, 5, 11)이라면 0.4 간격으로 [1. 1.4 1.8 2.2 2.6 3. 3.4 3.8 4.2 4.6 5.]가 반환된다. 위 코드에서는 n을 150으로 설정했으므로 1부터 5까지 일정한 간격으로 150개의 실수가 배열에 담겨 반환되고, 이것이 각 점의 $x$좌표가 된다. 다음은 그냥 참고사항으로 봐두면 될 것 같다.

* 세 번째 인자를 1로 전달하면 어떻게 될까? 이때는 그냥 시작점만 배열에 담겨 반환된다. 즉, 위 예에서는 [1.]이 반환된다.

* endpoint = False를 전달하면 양 끝이 포함되지 않지만, 디폴트값이 True이므로 여기서는 양 끝이 포함된다.

 

그리고 위 코드의 y = x**2 - 6*x + 10 + noise 부분을 보면 알 수 있듯이 점의 분포가 $y=x^2-6x+10$의 그래프를 흉내내게끔 했다. 다만 이차함수 그래프와 완벽히 일치하지는 않도록 하기 위해 난수로 만든 노이즈를 첨가했다. np.random.rand(n)은 0부터 1까지의 실수를 n개 반환하는데, 여기에서는 난수 생성 후 0.5를 빼서 노이즈의 범위를 -0.5부터 0.5까지로 바꿨다.

 

다음은 생성된 150개의 점을 그래프로 시각화한 것이다.

 

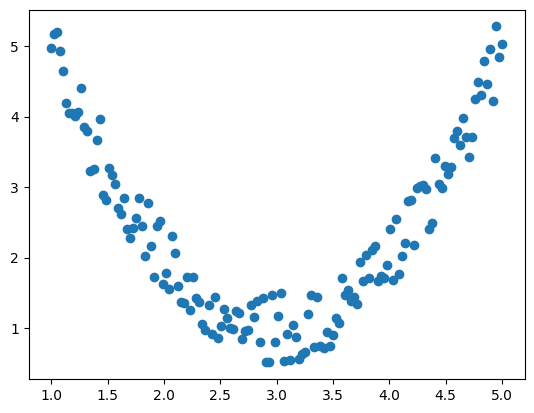
노이즈가 첨가되었기 때문에 이차함수 그래프와 완전히 일치하지는 않지만, 어느 정도 이차함수의 형태를 따르고 있음을 확인할 수 있다.

 

이제 이 문제를 다중 선형 회귀 문제로 변환해보자.

x_multi = np.array([x, x**2])

 

입력 데이터 $x$를 $x_1=x$, $x_2=x^2$으로 변환한다. 그리고 변환된 배열을 x_multi에 저장했다.

 

import numpy as np

W = np.zeros(shape=(1, len(x_multi)))  
b = 0
alpha = 0.005

y_pred = np.dot(W, x_multi) + b  
y_pred = y_pred.squeeze(0)  
MSE = np.sum((y - y_pred) ** 2) / n
print(f"초기 MSE: {MSE:.3f}")

epochs = 50000

for epoch in range(epochs):
    diff_W = -2/n * ((y - y_pred) @ x_multi.T)  
    diff_b = -2/n * np.sum((y - y_pred))

    W = W - alpha*diff_W
    b = b - alpha*diff_b

    y_pred = np.dot(W, x_multi) + b
    y_pred = y_pred.squeeze(0)
    MSE = np.sum((y - y_pred) ** 2) / n

    if (epoch+1) % 5000 == 0:
        print(f"epoch#{epoch+1}: W={np.round(W[0], 3)}, b={b:.3f}, MSE={MSE:.3f}")

print("\n최종 결과")
print(f"W = {W[0]}")
print(f"b = {b}")
print(f"MSE = {MSE}")

 

그 다음은 다중 선형 회귀의 코드를 그대로 긁어왔다. 다만 수정을 아예 안한건 아니고 자잘한 부분 몇 가지를 수정했다.

• 기존에 변수명 x라고 되어 있던 것을 모두 x_multi로 바꿨다.
• 학습률을 0.01에서 0.005로 줄였다. (이 예제에서는 0.01로 해도 오차 발산 현상 나타남)
• 에포크를 10,000회에서 50,000회로 늘렸다. (10,000회로 하면 만족스러운 결과가 나타나지 않음)

이런 자잘한 부분을 제외하고는 알고리즘이 바뀐 부분은 전혀 없다. 출력 결과는 다음과 같다.

초기 MSE: 7.001
epoch#5000: W=[-2.681  0.483], b=5.289, MSE=0.571
epoch#10000: W=[-4.402  0.755], b=7.672, MSE=0.208
epoch#15000: W=[-5.266  0.892], b=8.869, MSE=0.117
epoch#20000: W=[-5.7   0.96], b=9.470, MSE=0.094
epoch#25000: W=[-5.919  0.995], b=9.772, MSE=0.088
epoch#30000: W=[-6.028  1.012], b=9.924, MSE=0.087
epoch#35000: W=[-6.083  1.021], b=10.000, MSE=0.086
epoch#40000: W=[-6.111  1.025], b=10.038, MSE=0.086
epoch#45000: W=[-6.125  1.027], b=10.058, MSE=0.086
epoch#50000: W=[-6.132  1.028], b=10.067, MSE=0.086

최종 결과
W = [-6.1315695   1.02824871]
b = 10.067270243466911
MSE = 0.08609746352317205

 

가중치는 뒤에서부터가 고차항 계수이므로 최종 적합 결과는 $y=1.028x^2-6.132x+10.067$이다. 점들의 분포가 $y=x^2-6x+10$의 그래프에서 위아래로 살짝씩 벗어난 형태라는 점을 감안하면 꽤나 잘 적합된 결과라고 할 수 있다. MSE도 0.086으로 매우 작은 편이다.

 

그렇다면 적합 결과를 시각화 해보기로 하자.

plt.scatter(x, y, label="true")
plt.plot(x, y_pred, color="red", label="pred")
plt.legend()
plt.show()

 

plt.plot()은 원래 반듯한 선분을 그려주는 함수이다. x를 [1, 3, 5]로 주고 y를 [2, 4, 6]으로 주면, 두 점 (1, 2)와 (3, 4)를 잇는 선분이 하나 그려지고, 두 점 (3, 4)와 (5, 6)을 잇는 선분이 하나 그려지므로 총 2개의 선분이 그려진다. 이때, 숫자간 간격이 촘촘한 리스트를 x로 전달하면 매우 짧은 선분이 여러 개 생성되므로 곡선을 흉내낼 수 있다. 여기서는 1부터 5까지 150개의 수가 담겨있는 리스트를 x로 전달했으므로, 이웃한 숫자 간 간격은 0.0268 정도밖에 안 된다. 이러한 짧은 선분 149개로 이차곡선을 흉내내는 것은 충분하다.

 

그래프 출력 결과는 다음과 같다.

 

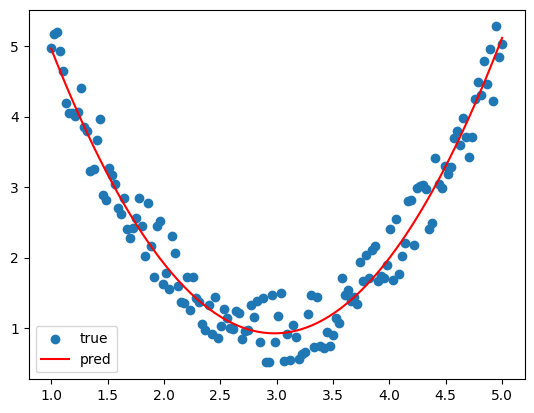
이차함수 그래프가 주어진 데이터에 꽤나 잘 적합되었음을 볼 수 있다.

즉, 선형 회귀를 제대로 이해했다면 다항 회귀는 전혀 어려운 것이 아니다. 다항 회귀는 단일 선형 회귀로 적합시키기 어려운 데이터를 다중 선형 회귀로 변형하여 적합시키는 개념이다.

 

② scikit-learn으로 수행하기

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import numpy as np

n = 150
x = np.linspace(1, 5, n)  # 양 끝점 포함하여 일정한 간격으로 n개의 수 반환
noise = np.random.rand(n) - 0.5  # [-0.5, 0.5] 범위의 노이즈 n개 생성
y = x**2 - 6*x + 10 + noise

poly = PolynomialFeatures(degree=2)  
x = poly.fit_transform(np.expand_dims(x, axis=1))  # 모든 x를 [1, x, x²]으로 변환

reg = LinearRegression()  # 선형 회귀 클래스 객체 저장
reg.fit(x, y)
W, b = reg.coef_, reg.intercept_  # coef_(계수), intercept_(절편)
y_pred = np.dot(x, W) + b
MSE = mean_squared_error(y, y_pred)

print(f"W = {W}")
print(f"b = {b}")
print(f"MSE = {MSE}")

 

사이킷런에서는 다항 회귀를 위한 전처리 툴을 제공한다. PolynomialFeatures 객체는 주어진 피처를 다항 회귀를 위한 형태로 변환한다. degree는 몇차함수로 적합시킬지 정하는 파라미터이므로, 이차함수로 적합시키고 싶으면 2를 전달하면 된다. 단, 피처는 2차원 배열 형태로 주어져야 하는데 np.linspace() 함수로 생성한 배열은 1차원이므로 np.expand_dims() 함수를 이용하여 2차원으로 늘려줘야 한다. 원래 차원이 (150,)인 데이터이므로 (1, 150)으로 늘리고 싶으면 axis=0을 전달하면 되고 (150, 1)로 늘리고 싶으면 axis=1을 전달하면 되는데, 여기서는 열벡터 형태로 전달해야 하므로 axis=1을 전달해 준다.

 

그 이후는 다중 선형 회귀 코드와 똑같이 따라가면 된다.

 

실행 결과는 다음과 같다.

W = [ 0.         -6.02160114  1.00695699]
b = 9.999303433046192
MSE = 0.07251062611687606

 

역시나 $y=x^2-6x+10$에 근사하게 가중치와 편향이 결정되었으므로 잘 적합되었음을 알 수 있다.

 

(2) 적합이 많이 될 수록 좋은 것인가? (과적합 문제)

다음과 같이 10개의 데이터 샘플이 주어졌다고 하자.

 

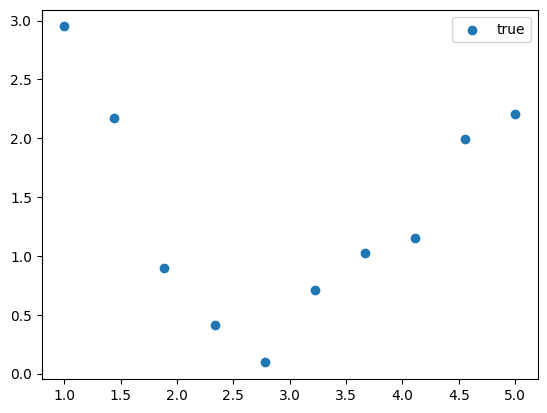
보니까 이것도 줄어들었다 늘어나는 형태니까 일차함수 적합은 어려울 것 같고... 이차함수로 적합하는게 좋을 것 같다. 그래서 다음과 같이 이차함수로 적합시켰다.

 

 

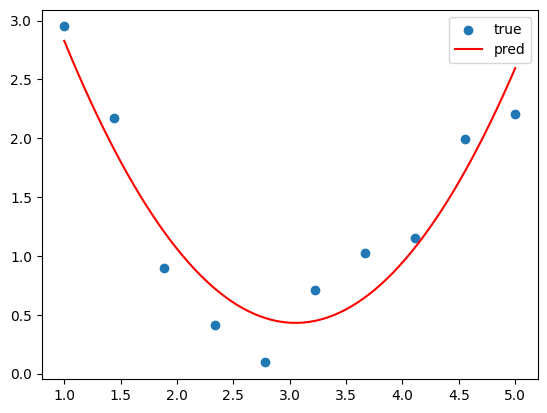
그런데 여기서 갑자기 이런 생각을 한다. "데이터 샘플이 10개니까, 9차함수로 적합을 시키면 오차가 하나도 안 생기게 적합시킬 수 있는거 아닌가?" 그래서 다음과 같이 9차함수로 데이터를 적합시켰다.

 

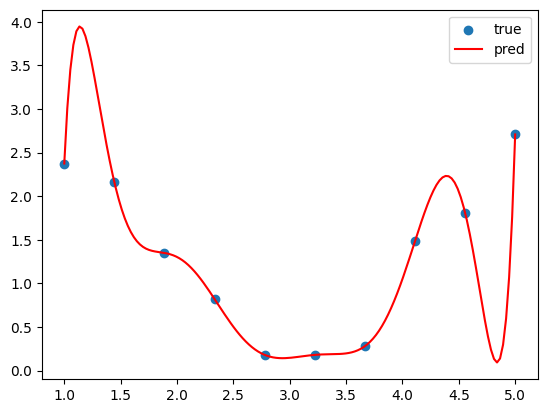
물론 이렇게 적합시키면 주어진 데이터들에 대해서는 오차가 없다. 하지만 이게 바람직하게 적합됐다고 할 수 있을까?

머신러닝 모델을 만드는 이유는 새로운 데이터가 주어졌을 때 이에 대한 예측을 잘 수행하는 것이지, 이렇게 이미 주어진 데이터들을 과도하게 맞춰주는게 목표가 아니다. 비유를 하자면 우리가 공부할 때 문제집을 푸는 이유는 처음 보는 시험 문제들을 잘 풀기 위함이지, 문제집의 정답만 달달 외우려고 푸는 것이 아니다. 문제집의 정답만 달달 외운다고 시험을 잘 보는게 아니듯이, 이미 주어진 데이터에만 과도하게 맞추다 보면 새로운 데이터에 대한 예측력은 오히려 떨어질 수 있다.

 

이렇게 모델이 학습 데이터에만 지나치게 적합되어 있는 것을 '과적합(overfitting)'이라고 한다. 머신러닝을 공부한다면 과적합이란 용어도 앞으로 밥 먹듯이 자주 보게 될 것이다. 겉보기에는 성능 지표 점수가 계속 올라가니까 좋은 것처럼 보일 수 있는데, 정작 새로운 데이터에 대해서는 형편 없는 성능 지표 점수를 보일 수 있기 때문에 피해야 하는 현상이다. 위 예시에서 과적합이 발생한 원인은 파라미터의 개수를 과도하게 늘린 것이라고 할 수 있다. 이차함수로 적합시켰으면 파라미터가 $w_1$, $w_2$, $b$로 총 3개 뿐이지만 9차함수까지 늘렸으니 파라미터가 $w_1$부터 $w_9$까지, 그리고 편향도 포함하면 총 10개가 된다. 이처럼 파라미터의 개수를 과도하게 늘린 것이 과적합의 원인이 될 수 있고, 반복 횟수(epoch)를 지나치게 많이 하는 것도 과적합을 유발할 수 있다. 또한 딥러닝 모델을 설계할 때 모델 구조를 지나치게 복잡하게 만들면 이 또한 과적합을 유발하는 원인이 된다.

 

과적합과 반대 개념으로 '과소적합(underfitting)'이라는 개념도 있다. 학습 데이터에라도 잘 맞춰져 있는 과적합과 달리, 과소적합은 학습 데이터에 조차도 제대로 맞춰져 있지 않은 현상이다. 과적합이 문제집만 달달 외워서 시험보러 가는 것이라면, 과소적합은 문제집을 거의 쳐다보지도 않고 시험보러 가는 것이라고 할 수 있겠다. 과소적합의 발생 원인은 과적합의 발생 원인을 반대로 하면 된다. 파라미터를 지나치게 적게 하는것, 반복 횟수를 지나치게 적게 하는 것, 모델 구조가 지나치게 단순한 것 등이 과소적합의 원인이 된다.

 

지금까지 설명한 과적합과 과소적합의 예를 그림으로 나타내면 다음과 같다.

이미지 출처 : https://medium.com/greyatom/what-is-underfitting-and-overfitting-in-machine-learning-and-how-to-deal-with-it-6803a989c76

 

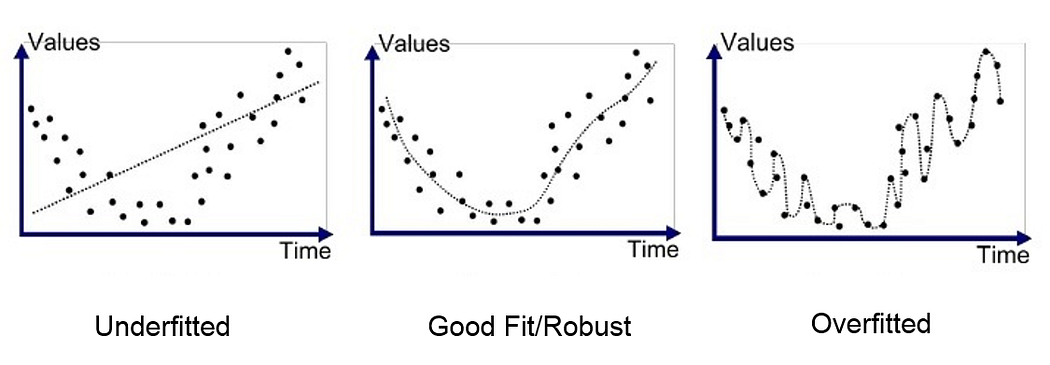
우리는 가운데 그림처럼 적당한 수준으로 모델을 피팅하는 것을 지향점으로 삼아야 한다. 오른쪽 그림처럼 과적합 되거나 왼쪽 그림처럼 과소적합 되는 것은 절대 바람직하지 못하다.

 

(3) 최소제곱법

다항 회귀를 다중 선형 회귀로 바라볼 수 있다고 했기 때문에, 다항 회귀에서도 다중 선형 회귀에서 제시한 최소 제곱법 공식을 적용할 수 있다. 다중 선형 회귀식 $\hat{\mathrm{y}}=\mathrm{x}\mathrm{w}$를 최적화 시키는 가중치 벡터는 $\mathrm{w}={\left({\mathrm{x}}^{\mathrm{T}}\mathrm{x}\right)}^{-1}{\mathrm{x}}^{\mathrm{T}}\mathrm{y}$이라고 했으며, 이때 편향도 $\mathrm{w}$에 포함된다는 이야기도 했었다. 수식 유도는 이미 다중 선형 회귀 포스팅에서 다 했으므로 여기서는 따로 유도하지 않고, 바로 코드 실습으로 들어간다.

import numpy as np

n = 150
x = np.linspace(1, 5, n)  
noise = np.random.rand(n) - 0.5  
y = x**2 - 6*x + 10 + noise

x_multi = np.array([x, x**2]).T
bias = np.ones((len(x_multi), 1))
x_multi = np.concatenate((x_multi, bias), axis=1)

w = np.dot(x_multi.T, x_multi)
w = np.linalg.inv(w)
w = np.dot(w, x_multi.T)
w = np.dot(w, y)

print(w)

 

np.ones() 모든 요소가 1인 배열을 반환하는 함수이다. 여기서는 주어진 데이터 샘플의 개수가 150개이므로 (150, 1) 크기의 이차원 배열을 생성하며, 그 요소는 모두 1로 한다. 이렇게 생성된 bias 배열을 기존의 x_multi에 이어붙이는데, 이때 사용하는 함수가 np.concatenate() 함수이다.

 

 

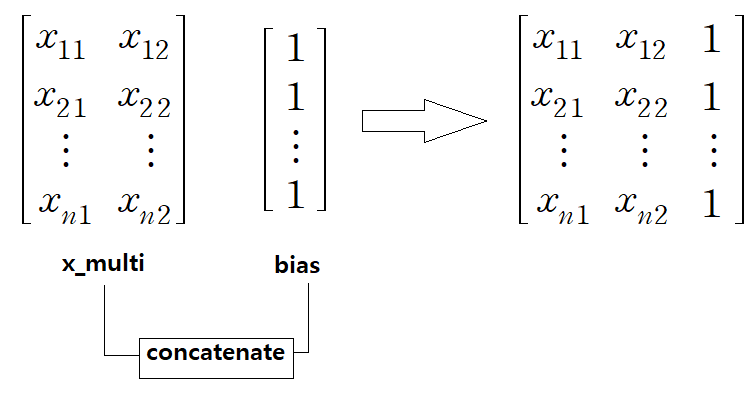
그러면 도대체 왜 오른쪽에 1을 덕지덕지 붙여주는 것이냐, 이것도 다중 선형 회귀 포스팅에서 이유를 찾을 수 있는데 다시 한 번 언급하자면 

 

$\mathrm{w}$에 편향 $b$가 포함되어 있기 때문에, 위 행렬곱 연산이 가능하려면 $\mathrm{x}$에 열이 하나 더 추가되어야 한다. 이때 선형 회귀식은 $y=w_1{x}_1+w_2{x}_2+w_3{x}_3+b$와 같은 꼴이므로 $b$에 곱해지는 수를 굳이 찾자면 1이다. 따라서 x_multi 행렬 오른쪽에 모든 요소가 1인 열벡터를 추가해주는 것이다.

 

위 코드의 출력 결과는 다음과 같다.

가중치([w1, w2, b]): [-6.05434818  1.01282715 10.00930603]

 

이번에도 $y=x^2-6x+10$의 그래프를 모방한 데이터 분포를 사용하였는데, $1.013x^2-6.054x+10.009$로 적합되었으므로 앞선 결과들처럼 꽤나 비슷하게 적합되었음을 알 수 있다.

 

② 릿지 회귀(Ridge Regression)

릿지 회귀나 뒤에 나오는 라쏘 회귀를 검색하면 가장 많이 나오는 키워드들이다 : 패널티(penalty), 규제(regularization)

규제라는 용어는 정규화, 정칙화라는 용어로도 번역된다. 도대체 뭘 규제하는거고 무슨 패널티를 준다는걸까? 지금부터 구체적으로 알아보도록 하자.

 

(1) L2 규제(L2 Regularization)

릿지 회귀는 L2 규제가 적용되는 회귀 방식이다. L2 규제에 대해 지금부터 알아보자.

 

다중 선형 회귀에서 오차 제곱 합은 다음과 같이 나타낼 수 있다고 하였다.

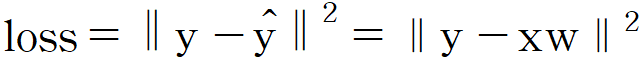
여기에 L2 규제(L2 정규화, L2 정칙화)를 추가하면 다음과 같아진다.

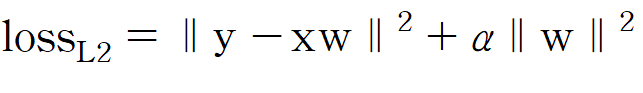
원래 식에 $\alpha \Vert \mathrm{w}{\Vert }^2$이 추가되었다($\alpha$는 양수). $\Vert \mathrm{w}{\Vert }^2$ 이 의미하는 바는 편향을 포함한 가중치 제곱 합($w_1^2+w_2^2+\cdots +w_n^2+b^2$)이므로, 가중치의 크기가 클수록 손실 함수의 값이 커질 것이다. 릿지 회귀 모델은 가중치의 크기를 줄이는 방향으로 학습을 진행하려고 할 것이다. 참고로 L2 규제는 이 규제를 개발한 사람의 이름을 따서 티호노프 규제(Tikhonov regularizaion)라고도 한다. 그런데 왜 이러한 규제를 적용하는 것일까?

 

L2 규제를 적용하는 이유를 한 줄로 요약하자면 과적합 방지 효과가 있기 때문이다. 다음 그림을 보자.

 

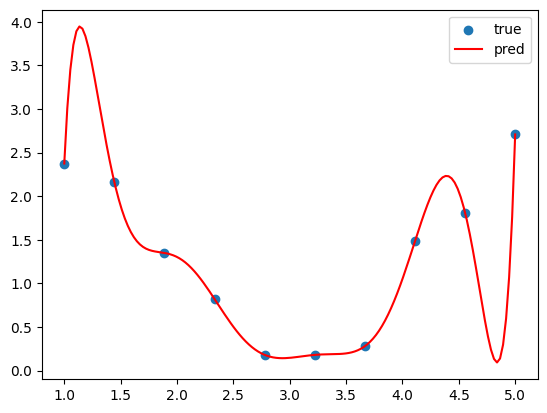
아까와 비슷하게 10개 데이터를 9차함수로 적합시킨 것이다. 그래프를 보면 알겠지만 9차함수의 그래프는 모든 점을 완벽하게 지나가고 있고, 매우매우 과적합된 상태이다. 그런데 이때 9차함수 각 항의 계수는 어떻게 될까?

 

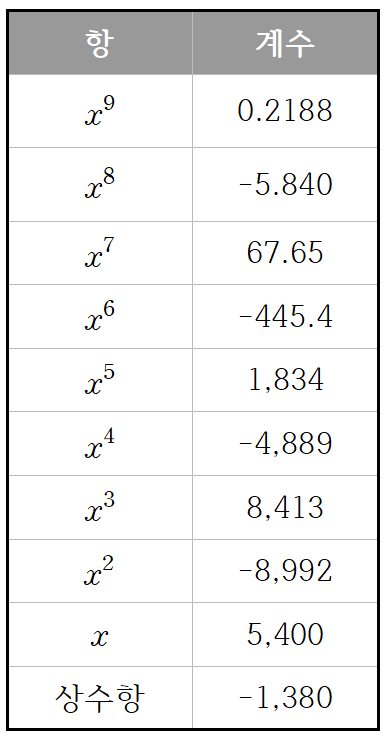
9차함수라는 함수 자체도 복잡한데, 그 안에 들어있는 계수들도 장난이 아니다... $x^5$부터는 계수가 아예 천 단위를 넘어가버린다. 이러한 상황에서 L2 규제가 과적합 방지 역할을 하는 것이다.

 

만약에 손실 함수를 기존 오차 제곱합 공식으로 했다고 하자. 그러니까 $\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}=\Vert \mathrm{y}-\mathrm{x}\mathrm{w}{\Vert }^2$로 했다고 하자. 위 적합 결과에 대해서 손실 함수 값은 0이다. 9차함수 그래프가 모든 데이터 점을 오차 없이 완벽하게 지나가기 때문이다.

 

하지만 여기에 $\alpha \Vert \mathrm{w}{\Vert }^2$라는 규제를 추가한 $\mathrm{l}\mathrm{o}\mathrm{s}{\mathrm{s}}_{\mathrm{L}2}=\Vert \mathrm{y}-\mathrm{x}\mathrm{w}{\Vert }^2+\alpha \Vert \mathrm{w}{\Vert }^2$를 사용하면 어떨까? 손실 함수 값이 매우매우 커진다. 물론 $\alpha$ 값이 얼마냐에 따라 달라지겠지만 일단 이를 고려하지 않는다면, $w$ 벡터에 포함된 11개의 값 중 절댓값이 가장 큰 값인 -8,992 하나만 제곱해도 벌써 천만 단위가 넘어간다. 11개의 값을 모두 제곱해서 더하면 억 단위의 어마어마하게 큰 수가 나온다. 따라서 일반 다항 회귀 기준으로는 손실 함수 값이 0이므로 최적화된 상태지만, 릿지 회귀 기준으로는 최적화와 거리가 한참 먼 상태가 되어버린다. 결국 릿지 회귀 모델을 최적화 하려면 실 데이터와 예측 데이터 간의 오차를 줄이는 것 뿐만 아니라 가중치의 크기를 줄이는 것까지도 신경을 써야한다.

 

여기서 $\Vert w{\Vert }^2$이 1만큼 증가할 때마다 손실 함수의 값이 $\alpha$만큼 증가하므로, $\alpha$는 규제의 강도를 조절하는 상수라고 할 수 있다. 즉, 상수 $\alpha$를 '규제 강도(regularization strength)'라고 한다. 규제 강도도 잘 설정해줘야 하는데, 규제 강도가 너무 약하면 과적합 방지 기능을 하기가 어렵고, 반대로 규제 강도가 너무 강하면 과소적합이 발생할 수 있다.

 

(2) 코드 실습 

scikit-learn으로 구현

사이킷런으로만 구현하고 넘어갈 것이다.

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
import numpy as np

# 시드값 지정 (난수 고정)
np.random.seed(seed=42)

# 데이터 생성
n = 10
x = np.linspace(1, 5, n)  
noise = np.random.rand(n) - 0.5  
y = 0.5*(x**2) - 3*x + 5 + noise

# 9차함수 적합을 위한 전처리
poly = PolynomialFeatures(degree=9)  
x_poly = poly.fit_transform(np.expand_dims(x, axis=1)) 

# 모델 생성 및 학습
reg = Ridge(alpha=1.0)  # 릿지 회귀 객체 생성 (규제 강도 1.0)
reg.fit(x_poly, y)
W, b = reg.coef_, reg.intercept_  # coef_(계수), intercept_(절편)
y_pred = np.dot(x_poly, W) + b
MSE = mean_squared_error(y, y_pred)

print(f"W = {W}")
print(f"b = {b}")
print(f"Loss = {MSE + np.dot(W.T, W)}")  # 릿지 회귀의 손실 함수

 

출력 결과

W = [ 0.         -0.01571456 -0.0340204  -0.04552899 -0.03885115 -0.01752584
 -0.0074672   0.01467348 -0.00405327  0.00032741]
b = 2.519557059204108
Loss = 0.019875454757930643

 

출력 결과를 보면, 가중치 값들이 꽤나 감소했음을 볼 수 있다. 릿지 회귀가 아닌 일반 다항 회귀를 사용했을 때는 천 단위 계수가 판을 쳤는데, 여기서는 기껏해야 0.01 단위이다. 릿지 회귀에서는 가중치의 크기가 손실 함수에 큰 영향을 미치기 때문에 가중치의 크기가 줄어드는 방향으로 최적화를 시킨 것이다.

 

이제 다음 코드를 실행시켜서 그래프를 출력해보자.

import matplotlib.pyplot as plt

graph_x = np.linspace(1, 5, 150)  # 곡선을 정밀하게 표현하기 위해 선분 구간을 149개로 나눔
graph_x_poly = poly.fit_transform(np.expand_dims(graph_x, axis=1))
graph_y = np.dot(graph_x_poly, W) + b

plt.scatter(x, y, label="true")
plt.plot(graph_x, graph_y, color="red", label="pred")
plt.legend()
plt.show()

 

출력 결과

 

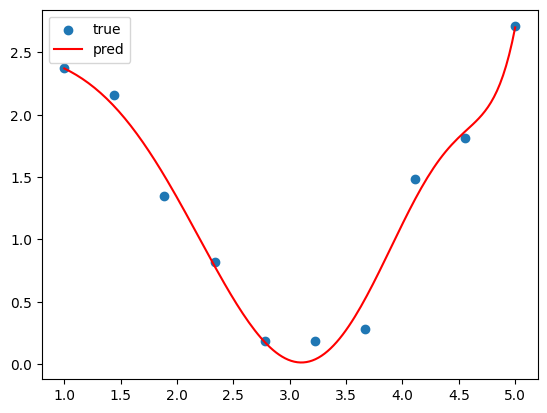
똑같이 9차함수로 적합시킨 것이지만, 모든 점을 지나게 하는 것보다는 확실히 더 적절하게 적합된 느낌이다. 이처럼 릿지 회귀가 과적합을 방지해준다는 사실을 눈으로 확인하였다.

 

그런데 여기서 사실 주의할 점은, 이게 그래도 9차함수인지라 $x$ 값이 조금만 범위에서 벗어나도 $y$ 값이 급발진 해버린다. 다음은 np.linspace()의 범위를 1부터 5.5까지로 늘렸을 때 그래프 출력 결과이다.

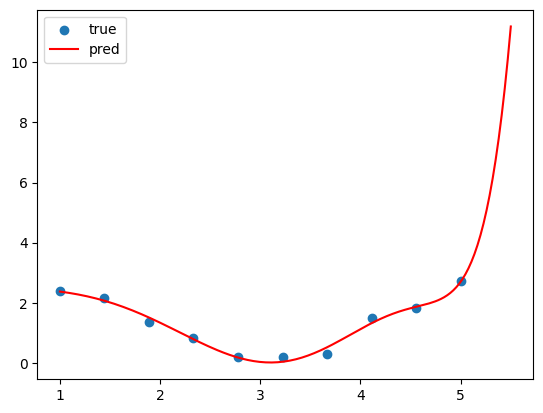
범위를 고작 0.5 늘렸을 뿐인데 그래프가 벌써 위로 솟구치고 있다. 따라서 $x$ 값의 범위가 1부터 5까지로 한정되어 있다는 보장이 있다면 L2 규제가 적용된 9차 다항 회귀를 사용해도 무방하지만, $x$가 이 범위 밖의 값도 가질 수 있다면 역시나 다항 회귀의 차수를 줄이는게 좋다.

 

(3) 릿지 회귀의 최적해

릿지 회귀도 행렬 연산으로 최적해를 구할 수 있다. 손실 함수 $\mathrm{l}\mathrm{o}\mathrm{s}{\mathrm{s}}_{\mathrm{L}2}$를 다시 보자.

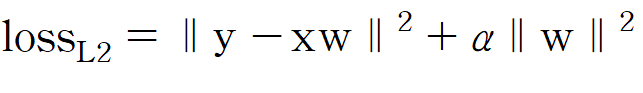
이를 $\mathrm{w}$에 대해 미분한 결과는 다음과 같다.

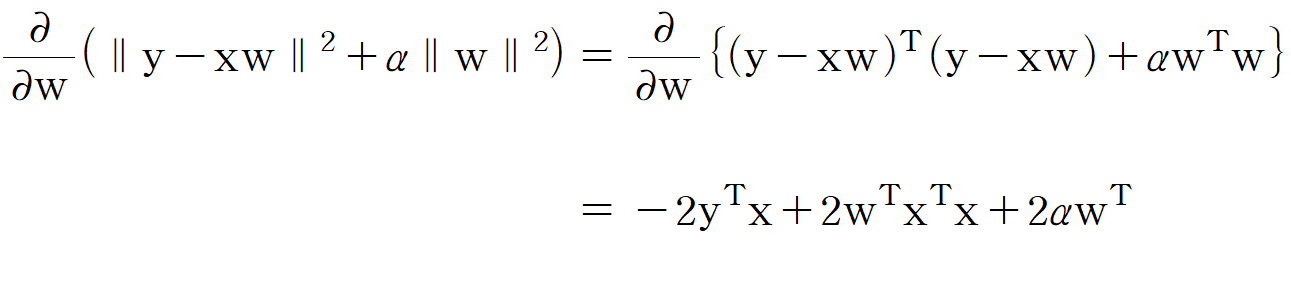
이 값이 0이므로 $-2{\mathrm{y}}^{\mathrm{T}}\mathrm{x}+2{\mathrm{w}}^{\mathrm{T}}{\mathrm{x}}^{\mathrm{T}}\mathrm{x}+2\alpha {\mathrm{w}}^{\mathrm{T}}=0$으로 등식을 세워놓고 $\mathrm{w}$에 대해 풀면 된다.

 

먼저 양변을 2로 나누면 다음과 같다.

$$-{\mathrm{y}}^{\mathrm{T}}\mathrm{x}+{\mathrm{w}}^{\mathrm{T}}{\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha {\mathrm{w}}^{\mathrm{T}}=0$$

그리고 $-{\mathrm{y}}^{\mathrm{T}}\mathrm{x}$를 우변으로 보내면 다음과 같다.

$${\mathrm{w}}^{\mathrm{T}}{\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha {\mathrm{w}}^{\mathrm{T}}={\mathrm{y}}^{\mathrm{T}}\mathrm{x}$$

좌변을 $w^T$로 묶을 수 있어보이는데 아직 걸리는 점이 있다. ${\mathrm{w}}^{\mathrm{T}}{\mathrm{x}}^{\mathrm{T}}\mathrm{x}$는 ${\mathrm{w}}^{\mathrm{T}}$가 앞쪽에 곱해져 있고 $\alpha w^T$는 ${\mathrm{w}}^{\mathrm{T}}$가 뒷쪽에 곱해져 있다. 행렬은 곱셈 순서를 바꾸면 결과가 달라질 수 있거나 곱셈 자체가 불가능해지는 성질이 있어서 이렇게 되면 좌변을 ${\mathrm{w}}^{\mathrm{T}}$로 묶을 수 없을 것 같다. 하지만 다행인 점은 $\alpha w^T$에서 $\alpha$는 상수이다. 따라서 둘의 위치를 바꿔서 ${\mathrm{w}}^{\mathrm{T}}\alpha$로 써도 무방하다. 이제 좌변을 ${\mathrm{w}}^{\mathrm{T}}$로 묶을 수 있게 됐다.

$${\mathrm{w}}^{\mathrm{T}}({\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha )={\mathrm{y}}^{\mathrm{T}}\mathrm{x}$$

이렇게 놓고 보니 뭔가 또 이상하다. ${\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha$에서 ${\mathrm{x}}^{\mathrm{T}}\mathrm{x}$는 행렬이고 $\alpha$는 스칼라인데 둘이 더한다는게 가능한건가? 당연히 불가능하다. 이 문제가 생긴 이유는 원래 ${\mathrm{w}}^{\mathrm{T}}\alpha$가 하나의 행렬이었는데 ${\mathrm{w}}^{\mathrm{T}}$으로 묶으면서 스칼라 $\alpha$ 혼자 분리된 채로 괄호 안에 들어갔기 때문이다. 이에 대한 해결책은 ${\mathrm{w}}^{\mathrm{T}}\alpha$에 항등행렬 $I$를 곱한 후 으로 ${\mathrm{w}}^{\mathrm{T}}$로 묶어주는 것이다. 

$${\mathrm{w}}^{\mathrm{T}}{\mathrm{x}}^{\mathrm{T}}\mathrm{x}+{\mathrm{w}}^{\mathrm{T}}\alpha \mathit{I}={\mathrm{y}}^{\mathrm{T}}\mathrm{x}$$ 

위 식을 ${\mathrm{w}}^{\mathrm{T}}$로 묶어주면 문제가 해결된다.

$${\mathrm{w}}^{\mathrm{T}}({\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha \mathit{I})={\mathrm{y}}^{\mathrm{T}}\mathrm{x}$$

양변의 뒷쪽에 ${({\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha \mathit{I})}^{-1}$을 곱해주자.

$${\mathrm{w}}^{\mathrm{T}}={\mathrm{y}}^{\mathrm{T}}\mathrm{x}{({\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha \mathit{I})}^{-1}$$

마지막으로 양변을 전치시켜준다.

$$\mathrm{w}={({\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha \mathit{I})}^{-1}{\mathrm{x}}^{\mathrm{T}}\mathrm{y}$$

${({\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha \mathit{I})}^{-1}$는 전치를 시켜도 자기 자신이다. ${\mathrm{x}}^{\mathrm{T}}\mathrm{x}$와 $\alpha I$는 모두 대칭 행렬이기 때문이다. 따라서 릿지 회귀의 최적해는 $\mathrm{w}={({\mathrm{x}}^{\mathrm{T}}\mathrm{x}+\alpha \mathit{I})}^{-1}{\mathrm{x}}^{\mathrm{T}}\mathrm{y}$가 된다.

 

그렇다면 이제 이를 코드로 구현해서 확인해보자. 다음은 9개의 데이터를 8차함수로 적합시키되, L2 규제를 적용해서 적합시킨 것이다. (원래 10개 데이터로 9차함수로 적합시키려고 했으나 행렬 안의 숫자가 너무 커져서 불안정한 탓인지 결과가 이상하게 나왔다. 8차함수까지는 결과가 제대로 나와서 8차함수로 한다.)

from sklearn.preprocessing import PolynomialFeatures
import numpy as np

# 시드값 지정 (난수 고정)
np.random.seed(seed=42)

# 데이터 생성
n = 9
x = np.linspace(1, 5, n)  
noise = np.random.rand(n) - 0.5  
y = 0.5*(x**2) - 3*x + 5 + noise

# 상수 정의
alpha = 1.0  # 규제 강도 
degree = 8  # 다항 회귀 차수

# 8차함수 적합을 위한 전처리
poly = PolynomialFeatures(degree=degree)  
x_poly = poly.fit_transform(np.expand_dims(x, axis=1))

# 최적해 계산
w = np.dot(x_poly.T, x_poly) + alpha*np.eye(degree+1) 
w = np.linalg.inv(w)
w = np.dot(w, x_poly.T)
w = np.dot(w, y)

print(w)

 

출력 결과

w = [ 0.72068258  0.59767312  0.38699157  0.10223181 -0.1457044  -0.14754776
  0.10344965 -0.02071705  0.00135865]

 

규제가 걸린 탓에 가중치가 전반적으로 1이 넘는것이 없다. 제대로 적합되었는지 그래프로 확인해보자.

 

import matplotlib.pyplot as plt

graph_x = np.linspace(1, 5, 150)  # 곡선을 정밀하게 표현하기 위해 선분 구간을 149개로 나눔
graph_x_poly = poly.fit_transform(np.expand_dims(graph_x, axis=1))
graph_y = np.dot(graph_x_poly, w)

plt.scatter(x, y, label="true")
plt.plot(graph_x, graph_y, color="red", label="pred")
plt.legend()
plt.show()

 

출력 결과

 

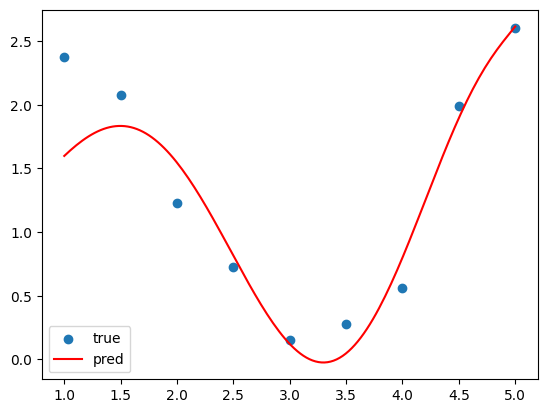
아.. 적합이 뭔가 살짝 잘못된 것 같다. 이유가 뭘까? 원인은 규제가 너무 강한 탓에 있었다. 앞서 말했듯이 규제가 너무 강하면 과소 적합이 발생하는데 이것이 딱 그 케이스이다. 규제가 너무 강한 탓에 가중치 크기를 줄이는데 신경을 너무 써서 데이터 샘플 오차를 줄이는 것은 신경을 쓰지 못한 것이다.

 

규제 강도를 0.1로 줄여봤더니 그래프가 다음과 같이 예쁘게 출력되었다.

 

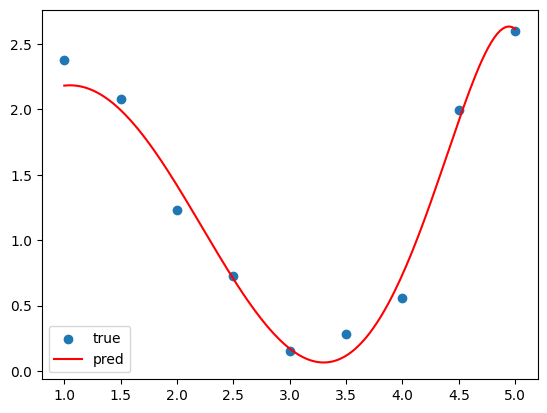
어느 하이퍼파라미터나 다 마찬가지지만, 그 값을 적당하게 설정해주는게 항상 중요하다. 여기서도 실습을 통해 적당한 규제 강도 설정이 중요하다는 것을 확인할 수 있었다.

 

③ 라쏘 회귀(Lasso Regression)

라쏘(Lasso)는 사람 이름 같은건 아니고 'Least Absolute Shrinkage and Selection Operator'의 줄임말이라고 한다. 라쏘 회귀도 릿지 회귀와 비슷하게 규제를 가하는 방식의 회귀이다. 릿지 회귀에서 적용하는 규제가 L2 규제라면, 라쏘 회귀에서 적용하는 규제는 L1 규제이다. 도대체 L2는 뭐고 L1은 뭐길래 이런 이름이 붙은거지? L1 규제에 대해 알아보기 전에 먼저 Lp-Norm이라는 개념에 대해 소개하려고 한다.

 

Lp-Norm은 다음과 같이 정의된다.

$$\Vert x{\Vert }_p={(|x_1{|}^p+|x_2{|}^p+\cdots +|x_n{|}^p)}^{\frac{1}{p}}$$

 

Lp-Norm의 한 종류인 L2-Norm은 다음과 같이 정의된다.

$$\Vert x{\Vert }_2=(|x_1{|}^2+|x_2{|}^2+\cdots +|x_n{|}^2)=\sqrt{x_1^2+x_2^2+\cdots +x_n^2}$$

그런데 L2-Norm은 유일하게 $\Vert x{\Vert }_2$에 붙는 2를 생략해서 쓸 수 있다. 따라서 다음과 같이 써도 된다.

$$\Vert x\Vert =\sqrt{x_1^2+x_2^2+\cdots +x_n^2}$$

릿지 회귀에서는 이 노름을 제곱해서 얻은 수로 규제를 적용하기 때문에 L2 규제라는 이름이 붙은 것이다.

 

라쏘 회귀에서 적용되는 L1 규제는 다음과 같은 L1-Norm을 사용한다.

$$\Vert x{\Vert }_1=|x_1|+|x_2|+\cdots +|x_n|$$

즉, ‖x‖_{1}은 벡터 내 모든 요소의 절댓값(Absolute)의 합과 같다. 라쏘 회귀에서는 이 값이 손실 함수 값에 반영되기 때문에 라쏘 회귀 모델은 이 값을 줄이는 방향으로 데이터를 적합시키려고 할 것이다.  따라서 'Least Absolute Shrinkage and Selection Operator'에서 'Least Absolute Shrinkage'가 이를 의미한다고 생각하면 된다.

 

그리고 릿지 회귀와 구별되는 라쏘 회귀의 중요한 특징을 하나 더 이야기하자면, 릿지 회귀는 가중치의 크기를 줄이기는 해도 가중치를 아예 0으로 만들어버리지는 않는다. 하지만 라쏘 회귀에서는 가중치를 0으로 만들어버리기도 한다. 이때, 0이 된 가중치와 곱해진 변수는 당연히 아무 의미가 없어지게 된다. 즉, 가중치를 0으로 만듦으로써 '변수 선택(Selection Operator)'의 기능을 수행하는 것이다.

 

사이킷런에서 라쏘 회귀의 손실 함수는 다음과 같이 정의된다.

$n$은 데이터 샘플의 개수를 의미한다. 저 $\frac{1}{2n}$은 위키피디아에서는 $\frac{1}{n}$으로 쓰고 어디는 $\frac{1}{2}$로 쓰고...(공부하면서 가장 짜증나는 부분 중 하나다. 그냥 좀 하나로 통일하지...) 어쨌든 뭐가 곱해졌는지가 중요한건 아니고 $\alpha \Vert w{\Vert }_1$이라는 규제가 붙었다는 점에만 신경을 쓰면 될 것 같다. 그리고 릿지에서는 $\frac{1}{2n}$이라는건 따로 안 붙었던 것 같은데... 왜 릿지는 안 붙고 이건 붙는지 모르겠지만 그런거 하나하나 깊게 파고들면 시간이 없으므로 패스

 

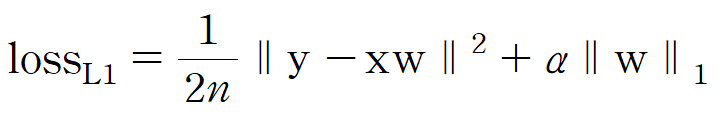
그런데 이 손실 함수에는 문제가 하나 있다. 손실 함수에 포함된 $\Vert \mathrm{w}{\Vert }_1$이 미분 불가능하다는 것이다. 따라서 이때까지 해왔던 것처럼 손실 함수를 가중치로 미분하고, 미분 부호의 반대 방향으로 가는 것을 반복해서 손실 함수 값이 최솟값을 갖도록 하는게 어렵다는 뜻이다. 따라서 라쏘 회귀에서는 경사 하강법이 아닌 다른 최적화 기법이 필요하다.

 

사이킷런 문서에 따르면 ' The implementation in the class Lasso uses coordinate descent as the algorithm to fit the coefficients.', 즉 Lasso 회귀를 사용할 때 최적화 알고리즘으로 coordinate descent(좌표 하강법)을 사용한다고 한다. 사실 블로그 주인도 좌표 하강법이 뭔지 잘 모른다. 나중에 알게 된다면 최적화 기법을 다루는 포스팅에서 한 번 다뤄보도록 하겠다.

 

마지막으로 사이킷런으로 라쏘 회귀를 구현하고 끝내려고 한다.

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import Lasso
from sklearn.metrics import mean_squared_error
import numpy as np

# 시드값 지정 (난수 고정)
np.random.seed(seed=42)

# 데이터 생성
n = 10
x = np.linspace(1, 5, n)  
noise = np.random.rand(n) - 0.5  
y = 0.5*(x**2) - 3*x + 5 + noise

# 9차함수 적합을 위한 전처리
poly = PolynomialFeatures(degree=9)  
x_poly = poly.fit_transform(np.expand_dims(x, axis=1)) 

# 모델 생성 및 학습
reg = Lasso(alpha=1.0)  # 라쏘 회귀 객체 생성 (규제 강도 1.0)
reg.fit(x_poly, y)
W, b = reg.coef_, reg.intercept_  # coef_(계수), intercept_(절편)
y_pred = np.dot(x_poly, W) + b
MSE = mean_squared_error(y, y_pred)

print(f"W = {W}")
print(f"b = {b}")
print(f"Loss = {MSE + np.dot(W.T, W)}")

 

아까 사이킷런으로 릿지 회귀를 구현한 코드에서 Ridge -> Lasso 로만 바꿔주면 된다.

 

출력 결과

W = [ 0.00000000e+00 -0.00000000e+00 -0.00000000e+00 -8.22900172e-02
 -1.21011088e-02  4.94786581e-03  8.84372699e-04  1.78254278e-05
 -1.17462916e-05 -3.83868692e-06]
b = 1.9887940668564563
Loss = 0.11330241348358595

 

릿지 회귀와 다르게 일부 가중치는 0이 되었음을 확인할 수 있다.

그래프는 아까와 똑같은 코드를 실행시켜서 띄워주면 된다.

 

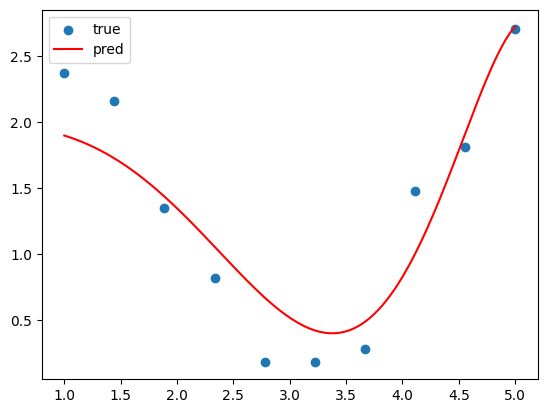
이번에도 적합 결과가 뭔가 좀 아쉽다. 릿지 회귀에서처럼 규제 강도를 0.1로 낮춰주면 해결된다.

 

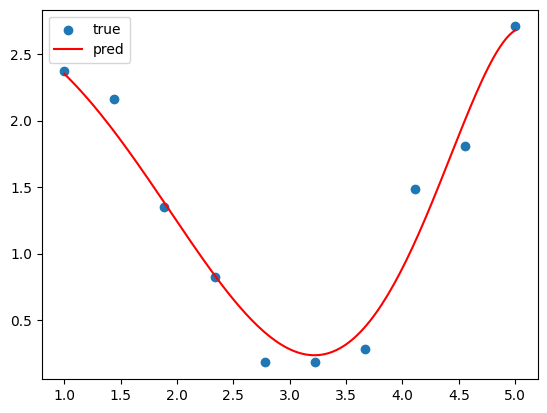
적합이 훨씬 그럴듯하게 되었음을 볼 수 있다.

 

④ 엘라스틱 넷(Elastic-Net)

라쏘 회귀까지 정리하고 끝내려고 했는데 엘라스틱 넷을 릿지, 라쏘랑 서로 다른 글에서 다루는건 이상한 것 같아서 엘라스틱 넷까지 여기에 포함시키기로 했다.

 

엘라스틱 넷은 릿지 회귀와 라쏘 회귀의 개념이 융합된 모델이다. 손실 함수는 다음과 같다.

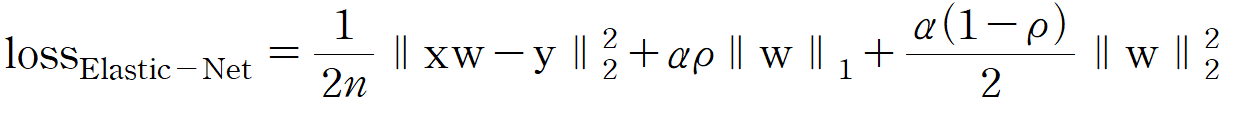
수식을 보면 알 수 있듯이 L1-Norm과 L2-Norm이 모두 포함되어 있다. 왜 L1-Norm에는 2를 안 나누고 L2-Norm에는 2를 나누지? 필자도 궁금하긴 하지만 이게 핵심은 아니기 때문에 일단 받아들이고 넘어가자. 챗지피티에게 물어봤더니 미분할 때 계수 맞춰주려고 그런거라는데, 일리는 있지만 어차피 $\Vert w{\Vert }_1$은 미분 안 되는거 아닌가? 공부를 하다보면 이렇게 미스테리한 부분이 참 많다. 어쨌든 엘라스틱 넷은 L1 규제와 L2 규제가 모두 포함되어 있다는 것이 가장 중요한 포인트이다.

 

$\alpha$는 릿지 회귀와 라쏘 회귀에서 그랬던 것처럼 규제 강도를 의미한다. $\rho$라는 파라미터가 새로 등장했는데 이는 위 수식에서 짐작할 수 있는 것처럼 L1 규제의 비율을 의미한다. 나는 또 여기서 이런 의문이 생겼다.

 

"$\rho =0.3$이라고 하면 손실 함수 뒷부분이 $0.3\alpha \Vert \mathrm{w}{\Vert }_1+0.35\alpha \Vert \mathrm{w}{\Vert }_2^2$이 되는데, 계수가 각각 0.3이랑 0.7이어야 L1 규제의 비율이 30%라고 할 수 있는거 아닌가..? 0.3이랑 0.35면 L1 규제의 비율이 46% 정도인거잖아"

 

라고 생각은 했는데 이것 또한 그냥 받아들이기로 했다. API 문서를 보면 이 $\rho$라는 파라미터의 이름이 코드에서는 'l1_ratio'라고 되어있다. 그 말인 즉슨 $\rho$가 0.3이면 'l1_ratio'가 0.3이라는 뜻이니 L1 규제의 비율이 30%라는 뜻이겠지. 어차피 실제로 코드 짤 때는 L1 규제가 실제로 30%로 들어가는지 46%로 들어가는지 관심이 없다. 일단 0.3으로 넣었다가 학습이 잘 되는 것 같으면 유지하고 아니면 바꾸는 식으로 하면 되는거지 L1 규제가 30% 들어가는지 46% 들어가는지는 전혀 관심을 가질 필요가 없다.

 

공부하면서 이런 미스테리들 때문에 포스팅 하는데도 어려움이 생기는데, 이런 미스테리에 하나하나 집착하면 시간이 너무 뺏긴다. 따라서 앞으로는 별로 안 중요한 것 같은 미스테리는 그냥 넘어가려고 한다.

 

당연한 사실이지만 $\rho =0$이면 L1 규제의 비중이 0%이므로 릿지 회귀가 되고, $\rho =1$이면 L1 규제의 비중이 100%이므로 라쏘 회귀가 된다.

 

마지막으로 사이킷런에서 엘라스틱 넷 모델을 사용한 코드를 보이고 포스팅을 마무리하겠다.

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import ElasticNet
from sklearn.metrics import mean_squared_error
import numpy as np

# 시드값 지정 (난수 고정)
np.random.seed(seed=42)

# 데이터 생성
n = 10
x = np.linspace(1, 5, n)  
noise = np.random.rand(n) - 0.5  
y = 0.5*(x**2) - 3*x + 5 + noise

# 9차함수 적합을 위한 전처리
poly = PolynomialFeatures(degree=9)  
x_poly = poly.fit_transform(np.expand_dims(x, axis=1)) 

# 모델 생성 및 학습
reg = ElasticNet(alpha=0.1, l1_ratio=0)  # 엘라스틱 넷 객체 생성 (규제 강도 0.1, L1 규제 비율 50%)
reg.fit(x_poly, y)
W, b = reg.coef_, reg.intercept_  # coef_(계수), intercept_(절편)
y_pred = np.dot(x_poly, W) + b
MSE = mean_squared_error(y, y_pred)

print(f"W = {W}")
print(f"b = {b}")
print(f"Loss = {MSE + np.dot(W.T, W)}")