2025. 3. 10. 21:44ㆍ머신러닝, 딥러닝 개념/지도 학습

이번 포스팅은 다음 교재의 내용을 참고해서 작성했다.
https://sebastianraschka.com/pdf/lecture-notes/stat479fs18/02_knn_notes.pdf
① k-최근접 이웃(k-Nearest Neighbor, kNN) 개요

k-최근접 이웃(이후부터는 kNN이라고 씀)의 개념은 간단하다. 위 그림에서 몇 가지 데이터가 주어져 있고, 각 데이터는 class A 또는 class B로 분류되어 있다. 이때, 미지의 데이터가 들어왔을 때 이 데이터가 어느 클래스에 속하는지를 어떻게 판단할까?
kNN에서는 미지의 데이터와 거리가 가장 가까운 k개의 데이터를 뽑아내고, 뽑아낸 데이터들 중 가장 많은 데이터가 속하는 클래스로 미지의 데이터를 분류한다.
예를 들어, 위 그림에서 k=3이라고 하자. 미지의 데이터와 가장 거리가 가까운 3개의 데이터를 뽑았더니 class A의 데이터가 1개, class B의 데이터가 2개였다. 그렇다면 미지의 데이터는 class B로 들어가게 되는 것이다.
k를 어떻게 설정하느냐에 따라 분류 결과가 달라질 수 있다. 만약에 k=3이 아니고 k=7이라고 해보자. 미지의 데이터와 거리가 가장 가까운 7개의 데이터 중 class A의 데이터가 4개, class B의 데이터가 3개이므로 이번엔 class A의 데이터가 더 많다. 따라서 미지의 데이터는 class A로 분류된다. kNN의 k는 하이퍼파라미터이므로, 경사 하강법의 학습률처럼 적절한 값 설정이 중요하다.
② kNN 알고리즘
지금부터 kNN 알고리즘을 파이썬 코드로 대략 구현해 볼 것이다.
데이터 세팅
import numpy as np
def random_label(point):
# x1과 x2의 합이 10 미만이면 90%의 확률로 class 0
# x1과 x2의 합이 10 이상이면 90%의 확률로 class 1
p = np.random.rand()
if point[0] + point[1] < 10:
if p <= 0.9:
return 0
else:
return 1
else:
if p <= 0.9:
return 1
else:
return 0
np.random.seed(42)
X = np.random.rand(100, 2)*10 # 훈련 데이터 100개, 난수 범위 [0, 10)
y = np.array([[random_label(point) for point in X]]).T
X_test = np.random.rand(10, 2)*10 # 테스트 데이터 10개, 난수 범위 [0, 10)
먼저 위와 같이 데이터를 만들었다.
- X에는 [$x_1$, $x_2$] 형태의 좌표 데이터 100개가 들어있으며, $x_1$과 $x_2$의 범위는 모두 [0, 10)이다. np.random.rand() 함수로 생성한 난수의 범위는 [0, 1)이지만 여기에 10을 곱해서 [0, 10)으로 범위를 확장시켰다.
- y는 X에 속하는 데이터들의 클래스(타깃값)가 리스트로 나열된 것이다. 각 데이터 0 또는 1이라는 클래스로 분류되며, 내가 만든 함수 random_label()를 통해 데이터마다 라벨이 임의로 지정된다.
- X_test에는 테스트 데이터의 좌표 데이터 10개가 들어있다.
import pandas as pd
df = pd.DataFrame(np.hstack((X, y)), columns=['x1', 'x2', 'y'])
df["y"] = df["y"].astype(int)
df
다음으로 데이터프레임을 만들었다. 피처 X 오른쪽에 타깃값 y가 존재하는 형태로 만들고 싶은데, 이렇게 두 배열을 옆으로 이어붙이고 싶을 때 사용하는 함수가 np.hstack()이다. 데이터프레임 생성 결과는 다음과 같다.

다음으로 X_test에 대해서도 데이터프레임을 만들고 결과를 확인해보자.
df_test = pd.DataFrame(X_test, columns=["x1", "x2"])
df_test
사실 이렇게 보면 눈에 잘 안 들어오긴 한다. 그래프로 시각화해보자.
import matplotlib.pyplot as plt
class0 = df[df["y"] == 0]
class1 = df[df["y"] == 1]
plt.scatter(class0["x1"], class0["x2"], color="blue", label="class 0")
plt.scatter(class1["x1"], class1["x2"], color="red", label="class 1")
plt.scatter(df_test["x1"], df_test["x2"], color="black", label="unknown", marker="^")
plt.legend()
plt.show()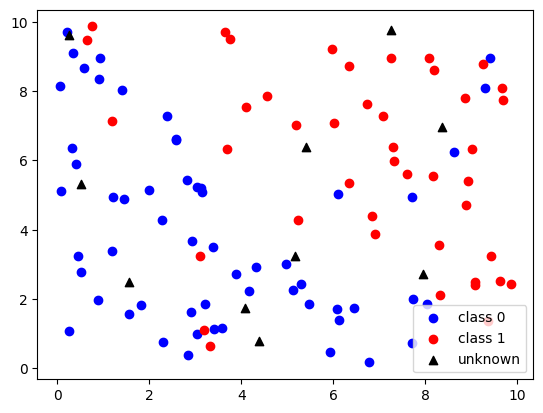
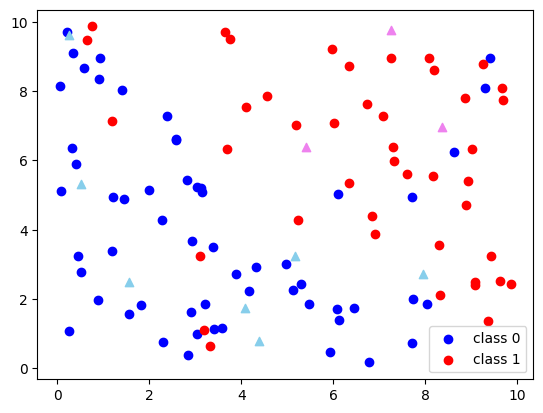
전반적으로 왼쪽 아래에는 클래스 0의 점이, 오른쪽 위에는 클래스 1의 점이 많이 분포해 있지만 불순물(?)들도 종종 섞여있다. 그거는 내가 일부러 라벨 매기는 함수 정의할 때 불순물도 섞이게끔 정의했기 때문이다.
검은색 세모 점이 테스트 데이터들에 해당하는 점들인데, 이 데이터를 kNN 알고리즘을 이용해서 클래스 0 또는 클래스 1로 분류하는 것이 목표이다.
데이터 사이의 거리
데이터 사이의 거리가 먼 지 가까운 지 판단하려면 거리에 대한 정의가 필요하다.
유클리드 거리(Euclidean Distance)
데이터 사이의 거리에 대한 가장 일반적인 정의가 유클리드 거리이다. 고등학교 수학에서도 점과 점 사이의 거리를 구할 때 사용한 방식이 유클리드 거리이다. 두 점 $p_1=(x_{1}, y_{1})$과 $p_2=(x_{2}, y_{2})$ 사이의 유클리드 거리는 다음과 같이 정의된다는 것을 알고 있을 것이다.
$$ d_{\rm euclidean}(p_1, p_2)=\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$$
만약에 두 점이 2차원보다 더 큰 차원인 $n$차원 점이라고 하자. 즉, $p_1=(x_{11}, x_{12}, \cdots, x_{1n})$이고 $p_2=(x_{21}, x_{22}, \cdots, x_{2n})$이라고 하자. 이때도 거의 비슷한 방식으로 계산하면 된다.
$$d_{\rm euclidean}(p_1, p_2)=\sqrt{(x_{21}-x_{11})^2 + (x_{22}-x_{12})^2 + \cdots +(x_{2n}-x_{1n})^{2}} = \sqrt{\sum_{i=1}^{n} \left(x_{2i}-x_{1i} \right)^{2}} $$
코드로 구현할 때도 데이터 사이의 거리는 유클리드 거리를 사용할 것이다. 따라서 다른 거리 정의는 알 필요가 없을 수도 있지만 교양 삼아 봐두기로 하자.
맨해튼 거리(Manhattan Distance)
맨해튼 거리는 택시 기하학으로도 잘 알려져 있다. 미국 뉴욕의 맨해튼에는 바둑판 격자 모양의 도로가 있는데, 이 맨해튼 도로의 한 지점에서 다른 지점까지 이동해야 하는 거리라는 뜻에서 맨해튼 거리라는 이름이 붙었다.
두 2차원 점 $p_1=(x_{1}, y_{1})$과 $p_2=(x_{2}, y_{2})$ 사이의 맨해튼 거리는 다음과 같이 정의된다.
$$ d_{\rm manhattan}(p_1, p_2)=|x_2-x_1| + |y_2-y_1|$$
두 $n$차원 점 $p_1=(x_{11}, x_{12}, \cdots, x_{1n})$과 $p_2=(x_{21}, x_{22}, \cdots, x_{2n})$ 사이의 맨해튼 거리는 다음과 같이 정의된다.
$$d_{\rm manhattan}(p_1, p_2)=|x_{21}-x_{11}| + |x_{22}-x_{12}| + \cdots +|x_{2n}-x_{1n}| = \sum_{i=1}^{n} |x_{2i}-x_{1i} |$$
사실 Lp-Norm 개념을 알고 있는 사람이라면 어느 정도 눈치챘을 법 한데(지도 학습 3편에서 다뤘음), 유클리드 거리는 L2-Norm이랑 유사하고 맨해튼 거리는 L1-Norm이랑 유사하다. 사실상 거의 같은 공식을 사용하고 있지만, 거리는 말 그대로 두 점 사이의 거리를 의미하는 것이고, 노름은 벡터의 크기를 의미한다는 점에서 개념적으로는 약간 차이가 있다.
민코프스키 거리(Minkowski distance)
노름에서 L2-Norm과 L1-Norm이 일반화된 개념인 Lp-Norm이 있는 것처럼, 거리에도 유클리드 거리와 맨해튼 거리가 일반화된 개념이 있다. 그것이 바로 민코프스키 거리이다.
두 2차원 점 $p_1=(x_{1}, y_{1})$과 $p_2=(x_{2}, y_{2})$ 사이의 민코프스키 거리는 다음과 같이 정의된다.
$$ d_{\rm minkowski}(p_1, p_2)=\left(|x_2-x_1|^{p} + |y_2-y_1|^{p} \right)^{\frac{1}{p}}$$
두 $n$차원 점 $p_1=(x_{11}, x_{12}, \cdots, x_{1n})$과 $p_2=(x_{21}, x_{22}, \cdots, x_{2n})$ 사이의 민코프스키 거리는 다음과 같이 정의된다.
$$d_{\rm minkowski}(p_1, p_2)=(|x_{21}-x_{11}|^p + |x_{22}-x_{12}|^p2 + \cdots +|x_{2n}-x_{1n}|^{p})^{\frac{1}{p}} = \left( \sum_{i=1}^{n} \left|x_{2i}-x_{1i} \right|^{p} \right)^{\frac{1}{p}}$$
이때, $p=2$이면 유클리드 거리, $p=1$이면 맨해튼 거리이다. 상술했듯이 $p=2$인 유클리드 거리가 가장 일반적으로 쓰이는 거리의 정의이다.
1-Nearest Neighbor(NN)
가장 간단한 1NN부터 구현해보자. 즉, 미지의 점과 가장 가까운 점 하나만 고려하는 것이다.
먼저 유클리드 거리를 계산하는 함수를 정의한다.
$$d_{\rm euclidean}(p_1, p_2) = \sqrt{\sum_{i=1}^{n} \left(x_{2i}-x_{1i} \right)^{2}} $$
이므로 이를 그대로 넘파이 코드로 옮겨놓으면 된다.
def euclidean_distance(a, b):
return np.sqrt(np.sum((b-a)**2))
이제 이 유클리드 거리 함수를 이용하여 1NN을 수행하는 알고리즘을 짜보자.
y_test = np.array([]) # 테스트 데이터의 클래스 리스트
# 테스트 데이터 10개에 대한 반복문
for test_point in X_test:
closest_point = None # 가장 가까운 점
closest_label = None # 가장 가까운 점의 클래스
closest_distance = np.inf # 가장 가까운 점과의 거리
# 입력 데이터 100개에 대한 반복
for input_point, input_label in zip(X, y):
distance = euclidean_distance(test_point, input_point) # 유클리드 거리 계산
# 만약에 distance가 현재 최단 거리보다 짧으면 정보 갱신
if closest_distance > distance:
closest_point = input_point
closest_label = input_label
closest_distance = distance
y_test = np.append(y_test, [closest_label]) # 가장 가까운 점의 클래스를 배열에 추가
y_test = np.expand_dims(y_test, axis=1) # y의 차원 확장 (10,) -> (10, 1)
df_test["y"] = y_test.astype(int) # 클래스를 정수로 만들어 df_test에 덧붙임
코드 설명은 주석으로 다 써놨으니 아마 이해하기 어렵지 않을 것 같다.
하나만 보자면 내부 반복문에서 zip()이라는 함수가 사용되었는데, X와 y에서 동시에 데이터를 꺼낼 필요가 있으면 이렇게 zip() 함수를 이용해 두 배열을 묶어주면 된다. 그러면 첫 번째 반복에서는 input_point=X[0], input_label=y[0]이고 두 번째 반복에서는 input_point=X[1], input_label=y[1]이 되는 식으로 반복이 진행된다.
최종 결과, 라벨값이 df_test에 덧붙여졌다. 이를 직접 확인해보자.
df_test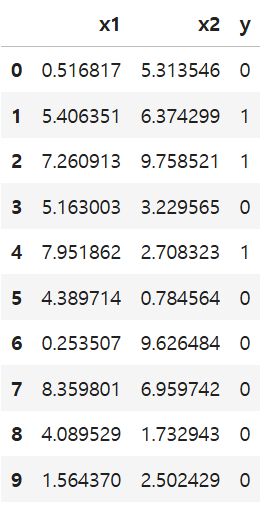
이렇게 알고리즘에 의해 덧붙여진 라벨값에 df_test에 덧붙여졌음을 확인할 수 있다. 대강 봐도 x1과 x2의 합이 크면 클래스 1로, 작으면 클래스 0으로 분류되는 경향이 있지만 예외적인 경우(7번)도 있기는 하다.
마지막으로 그래프로 시각화해서 분류 결과가 어떻게 되었는지 한 눈에 살펴보자.
import matplotlib.pyplot as plt
class0_test = df_test[df_test["y"] == 0]
class1_test = df_test[df_test["y"] == 1]
plt.scatter(class0["x1"], class0["x2"], color="blue", label="class 0")
plt.scatter(class1["x1"], class1["x2"], color="red", label="class 1")
plt.scatter(class0_test["x1"], class0_test["x2"], color="skyblue", marker="^")
plt.scatter(class1_test["x1"], class1_test["x2"], color="violet", marker="^")
plt.legend()
plt.show()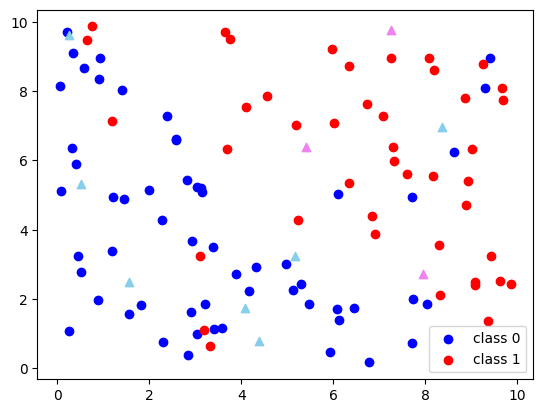
시각화 결과, 의도한대로 분류가 잘 되었음을 확인할 수 있다.
그림에서 가장 오른쪽에 있는 세모의 경우, 주변에는 빨간색 점이 더 많긴 하지만 가장 가까운 점이 파란색이라서 클래스 0으로 분류되었다. 이 경우, k값을 늘려주면 클래스 1로 분류 결과가 바뀔 가능성이 높다.
이번에는 k가 1보다 큰 일반적인 경우에 대해 kNN 알고리즘을 어떻게 구현할 수 있는지 알아보자.
나이브(Naive)하게 구현하기 1
naive는 한국어로 순진한, 천진난만한 이런 뜻이다. 따라서 구현이 나이브하다는건 구현 방식이 단순하다는 뜻으로 이해하면 될 것 같다. 나이브한 구현은 구현 자체가 매우 쉽다는 장점이 있지만 시간 복잡도 측면에서 비효율적인 경우가 많다. 따라서 실행 시간이 중요한 경우에는 어렵더라도 더 효율적인 알고리즘을 고려해봐야 한다.
두 가지 나이브한 구현 방법을 제시할 것이다. 먼저 첫 번째 나이브한 방법이다.
def naive_knn_1(X, y, test_point, k=3):
knn_idx = np.array([]) # 가장 가까운 k개의 점의 인덱스를 저장하는 배열
knn_label = np.array([]) # 가장 가까운 k개의 점의 클래스를 저장하는 배열
# knn_idx이 k개만큼 채워질 때까지 하나하나씩 채운다.
while len(knn_idx) < k:
closest_idx = None # 가장 가까운 점의 인덱스(그러니까 배열에서 몇 번째에 있는지)
closest_label = None # 가장 가까운 점의 클래스
closest_distance = np.inf # 가장 가까운 점과의 거리
# 입력 데이터 100개에 대한 반복
for idx, (input_point, input_label) in enumerate(zip(X, y)):
# 이미 knn_idx에 포함되어 있으면 스킵 (중복 추가 방지)
if idx in knn_idx:
continue
distance = euclidean_distance(test_point, input_point) # 유클리드 거리 계산
# 만약에 distance가 현재 최단 거리보다 짧으면 정보 갱신
if closest_distance > distance:
closest_idx = idx
closest_label = input_label
closest_distance = distance
knn_idx = np.append(knn_idx, [closest_idx]) # 가장 가까운 점 인덱스 추가
knn_label = np.append(knn_label, [closest_label]) # 가장 가까운 점 클래스 추가
knn_label = knn_label.astype(int) # knn_label을 정수형 배열로 변환
ret = np.bincount(knn_label).argmax() # knn_label의 최빈값 (최빈값이 미지 데이터의 클래스가 됨)
return ret
요약하자면, 바깥쪽 while 반복문을 한 번 돌면 가장 가까운 점의 인덱스와 클래스가 저장되고, 두 번째 돌면 그 다음으로 가까운 점의 인덱스와 클래스가 저장되고(가장 가까운 점은 continue로 제외되기 때문에), 세 번째 돌면 그 다음으로 가까운 것을 저장하는 방식이다.
점의 좌표 대신에 인덱스를 도입한 이유는 좌표가 완전히 같은 점이 2개 이상 존재할 수 있기 때문이다. 물론 여기에서는 점의 좌표가 다 실수로 되어있어서 동일한 점이 나올 확률은 거의 없긴 한데, 만약에 점의 좌표가 정수라면 필수적으로 고려해줘야 하는 부분이다.
그리고 ret = np.bincount(knn_label).argmax() 부분을 주목할만한데, 이 코드의 목적은 최빈값을 뽑아내는 것이지만 최빈값을 뽑아내는 원리를 간단한 코드로 보이고 넘어가려고 한다.
a = np.array([0, 0, 0, 1, 2, 2, 2, 2, 3, 4, 4, 9])
print(np.bincount(a)) # np.bincount(a) : 배열 a 안에 있는 요소들의 빈도 배열
print(np.bincount(a).argmax()) # np.bincount(a)[i]가 최대가 되도록 하는 i
출력 결과
[3 1 4 1 2 0 0 0 0 1]
2
출력 결과에서 짐작할 수 있는 사실이지만, a에 음수 또는 실수가 들어있으면 np.bincount() 함수를 사용할 수 없다. 사용하려고 하면 에러가 발생한다.

그래서 아까 제시한 코드에서도 knn_label을 정수형 배열로 바꾸는 코드가 없으면 에러가 발생한다.
다음으로는 naive_knn_1() 함수로 kNN 알고리즘을 수행하고 그 결과를 데이터프레임으로 출력하는 코드이다.
y_test = np.array([]) # 테스트 데이터의 클래스 리스트
# 테스트 데이터 10개에 대한 반복문
for test_point in X_test:
label = naive_knn_1(X, y, test_point, k=3)
y_test = np.append(y_test, label)
y_test = np.expand_dims(y_test, axis=1) # y의 차원 확장 (10,) -> (10, 1)
df_test["y"] = y_test.astype(int) # 클래스를 정수로 만들어 df_test에 덧붙임
df_test
출력 결과
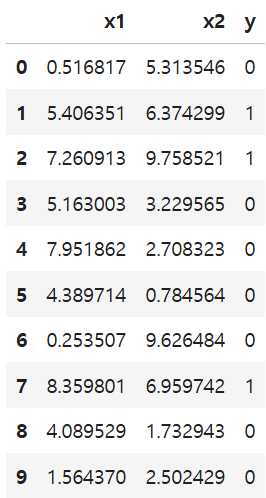
k = 1로 했을 때와 차이가 있을까? 한 번 비교해보자.
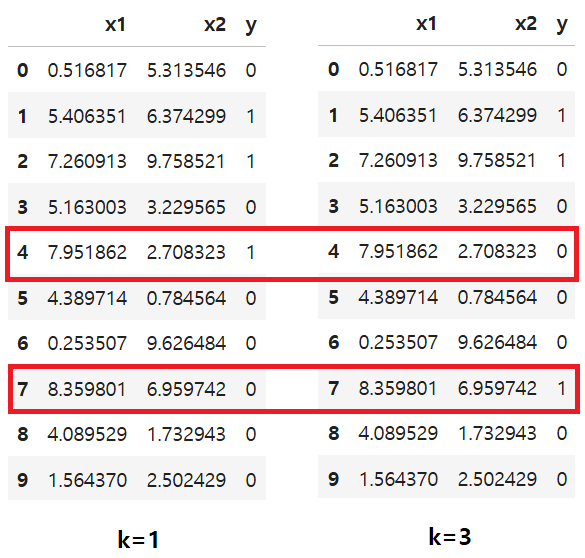
다른건 결과가 안 바뀌었는데, 4번 점과 7번 점의 결과가 달라졌다. 이를 시각화를 통해 확인해보자.
시각화 코드는 1NN에서의 시각화 코드와 완전히 동일하다.
출력 결과
k = 1일 때와 비교했을 때 2개 점의 클래스가 달라졌을 것이다. 직접 비교해보면 다음과 같다.
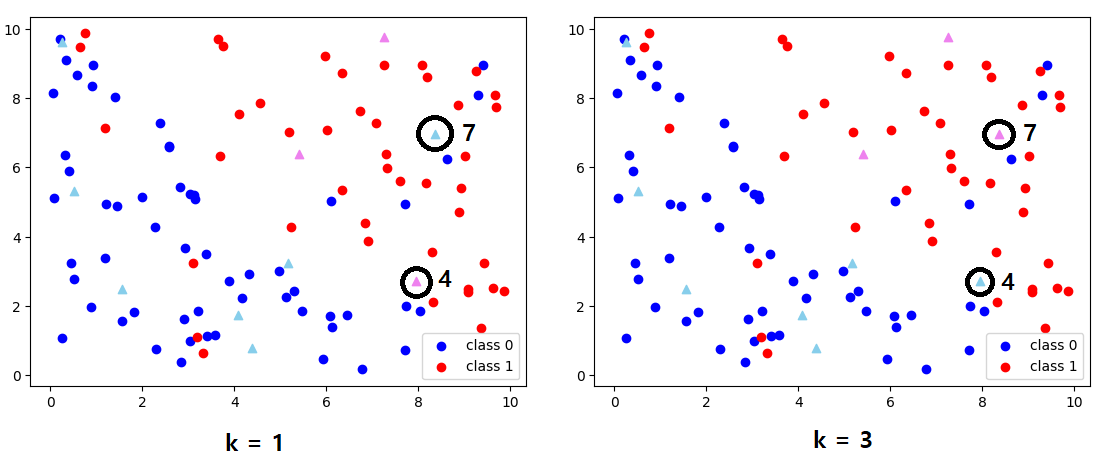
4번 점의 클래스가 1에서 0으로 바뀌었고 7번 점의 클래스가 0에서 1로 바뀌었다고 했는데 시각화를 통해 이를 직접 확인할 수 있었다.
나이브(Naive)하게 구현하기 2
두 번째 나이브한 구현 방법은 첫 번째에서 구현한 것과 반대의 느낌으로 돌아간다. 코드를 보자.
def naive_knn_2(X, y, test_point, k=3):
knn_idx = np.arange(len(y)) # [0, 1, ..., 99]
knn_label = y.squeeze() # 1차원으로 줄인 타깃값 배열 (100, 1) -> (100,)
# knn_idx이 k개로 줄어들 때까지 하나하나 삭제한다.
while len(knn_idx) > k:
farthest_idx = None # 가장 먼 점의 인덱스(그러니까 배열에서 몇 번째에 있는지)
farthest_distance = 0 # 가장 먼 점과의 거리
# 입력 데이터 100개에 대한 반복
for idx, input_point in enumerate(X):
if idx not in knn_idx:
continue
distance = euclidean_distance(test_point, input_point) # 유클리드 거리 계산
# 만약에 distance가 현재 최장 거리보다 길면 정보 갱신
if distance > farthest_distance:
farthest_idx = idx
farthest_distance = distance
# 마스크 연산을 통한 삭제
mask = knn_idx != farthest_idx
knn_idx = knn_idx[mask]
knn_label = knn_label[mask]
knn_label = knn_label.astype(int) # knn_label을 정수형 배열로 변환
ret = np.bincount(knn_label).argmax() # knn_label의 최빈값 (최빈값이 미지 데이터의 클래스가 됨)
return ret
naive_knn_1() 함수는 knn_idx와 knn_label을 비워놓은 상태에서 최단 거리에 해당하는 점을 추가해 나가는 알고리즘이었다면, naive_knn_2() 함수는 knn_idx와 knn_label을 꽉 채워놓은 상태에서 가장 멀리 떨어진 점을 하나씩 삭제해 나가는 알고리즘이다.
다른건 볼 건 없는데 '마스크 연산을 통한 삭제' 부분만 한 번 보자.
만약에 미지의 점과 가장 먼 점이 3번 인덱스의 점이라고 하자. 그렇다면 farthest_idx에는 3이 저장되어 있을 것이다.
knn_idx는 원래 [0, 1, ..., 99]인데 여기서는 설명의 편의상 5번까지만 있다고 하자([0, 1, 2, 3, 4, 5]). 그렇다면 knn_idx != farthest_idx는 [0, 1, 2, 3, 4, 5] != 3이 되는데, 이 결과는 [True, True, True, False, True, True]이다. 각 요소들에 대해 '!= 3' 연산을 적용했을 때 True 또는 False 여부를 배열로 반환한 것이라고 생각하면 된다.
다른 넘파이 배열에 이 마스크 배열을 적용하면 False가 저장된 위치(여기서는 3번)에 있는 요소가 삭제된다.
따라서 knn_idx[mask]라고 하면 knn_idx 배열에서 3번 인덱스 요소가 삭제된 배열이 반환되고, knn_label[mask]라고 하면 knn_label 배열에서 3번 인덱스가 삭제된 배열이 반환되는 것이다. 이런 식으로 삭제를 구현할 수 있다. 물론 이렇게 안 하고 np.delete() 같이 요소를 삭제해주는 함수를 사용할 수 있지만, 삭제할 때는 마스크 배열을 사용하는 것이 성능 면에서 더 효율적이라고 한다.
출력 결과는 naive_knn_1()을 사용한 것과 똑같이 나오므로 굳이 여기서 또 쓰지는 않으려고 한다.
힙(Heap) 이용하기
naive_knn_1() 함수의 경우, 외부 반복문의 순회 횟수는 $k$이고 내부 반복문의 순회 횟수는 $n$이므로 시간 복잡도는 $O(k \times n)$이다.
naive_knn_2() 함수의 경우, 외부 반복문의 순회 횟수는 $n-k$이고 내부 반복문의 순회 횟수는 $n$이므로 시간 복잡도는 $O((n-k) \times n)$이다.
$0<k<n$이므로 이 두 함수는 모두 $O(n)$과 $O(n^2)$ 사이의 성능을 보인다. 다만 naive_knn_1() 함수는 $k$가 작을수록 성능이 좋아지고 naive_knn_2() 함수는 $k$가 클수록 성능이 좋아진다는 차이가 있다.
힙을 이용하면 시간 복잡도가 $O(k \log (n))$(최소 힙을 이용했을 때) 또는 $O((n-k) \log (n))$(최대 힙을 이용했을 때)이므로 최악의 경우에도 $O(n \log n)$의 성능을 보장받을 수 있다. 최대 힙은 자료구조를 배웠다면 알만한데, 몇 가지 자료구조 개념에 대해 간단히 살펴보고 넘어가자. (자료구조 포스팅은 아니니 간단히 설명하고 넘어갈 것이다.)
- 큐(Queue) : 데이터를 꺼낼 때, 먼저 들어온 데이터를 먼저 꺼내는 선입선출(First In First Out, FIFO) 방식의 자료구조이다.
- 우선순위 큐(Priority Queue) : 데이터를 꺼낼 때, 들어온 순서와 상관 없이 우선순위가 가장 높은 데이터를 먼저 꺼내는 방식의 자료구조이다.
- 힙(Heap) : 여러 개의 값 중에서 가장 크거나 가장 작은 값을 빠르게 찾기 위해 고안된 자료구조로, 우선순위 큐를 구현하기 위한 도구로 사용된다. 힙은 항상 완전 이진 트리(Complete Binary Tree)여야 한다.
- 최대 힙(Max-Heap) : 루트 노드의 값이 최댓값이고, 부모 노드의 값이 자식 노드의 값보다 작지 않은 형태의 힙이다.
- 최소 힙(Min-Heap) : 루트 노드의 값이 최솟값이고, 부모 노드의 값이 자식 노드의 값보다 크지 않은 형태의 힙이다.
최소 힙과 최대 힙을 그림으로 표현하면 다음과 같다.
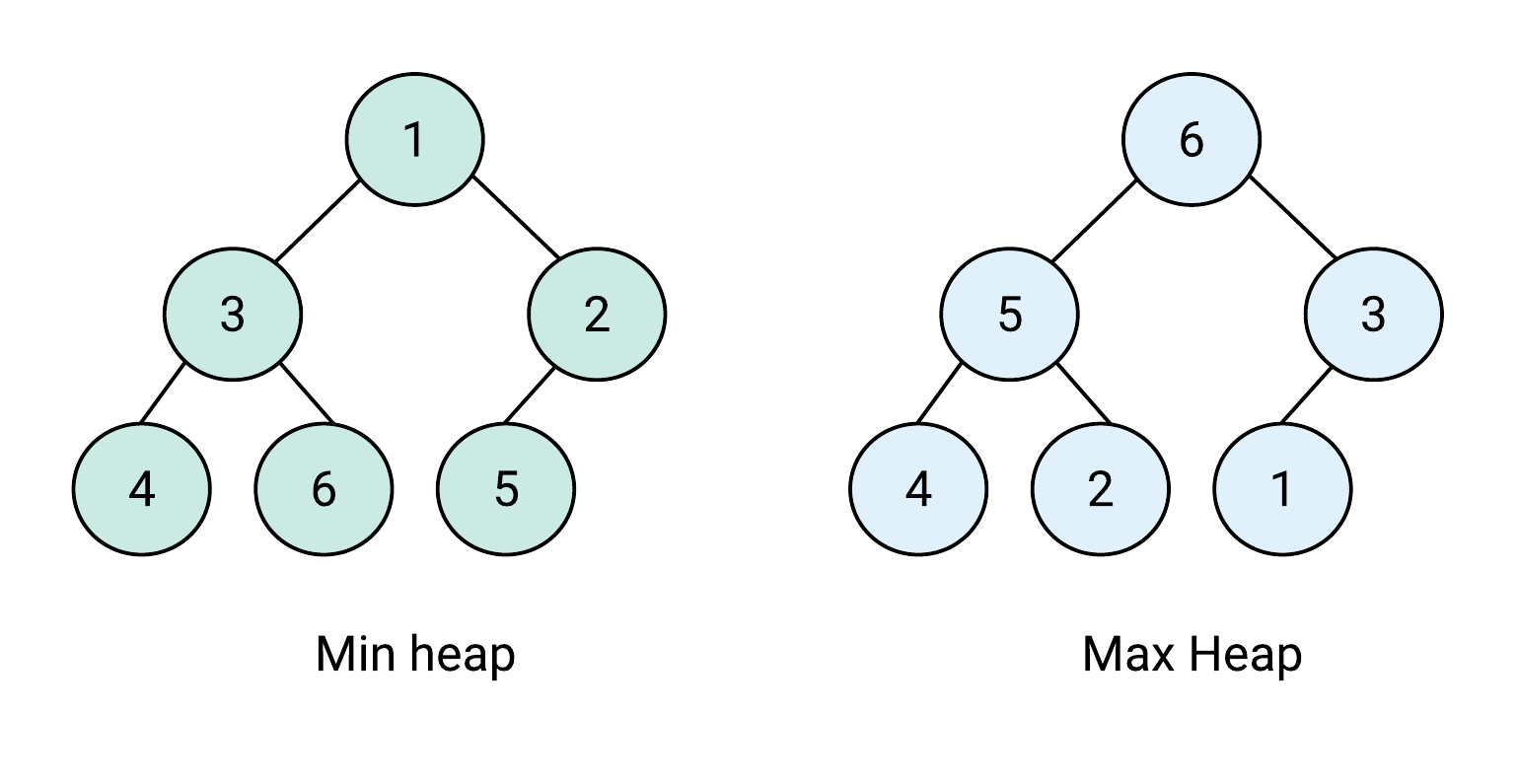
여기서는 최소 힙으로 구현한 결과를 자세히 설명하고, 최대 힙으로 구현한 것은 코드만 보여주고 넘어가려고 한다. 파이썬 내장 라이브러리 heapq를 import 해오면 힙을 사용할 수 있다.
import heapq
def min_heap_knn(X, y, test_point, k=3):
# 힙으로 사용할 리스트
# 입력 데이터들을 힙에 넣어준다.
heap = [
(euclidean_distance(test_point, input_point), input_label[0])
for input_point, input_label in zip(X, y)
]
heapq.heapify(heap) # 최소 힙 성질을 만족하도록 재구조화
# 거리가 가장 가까운 k개의 데이터를 꺼내고, 그 레이블 값을 knn_label 배열에 넣어준다.
knn_label = np.array([])
for _ in range(k):
label = heapq.heappop(heap)[1]
knn_label = np.append(knn_label, label)
knn_label = knn_label.astype(int)
ret = np.bincount(knn_label).argmax()
return ret
나이브하게 구현할 때보다 코드가 훨씬 간결해졌다.
위 코드에서 heap은 일반 리스트지만 heapq 라이브러리에 내장된 함수들을 이용해서 힙처럼 다룰 수 있다.
heapq.heappush() 함수는 힙에 데이터를 넣어주는 함수이고, heapq.heappop() 함수는 힙에서 데이터를 꺼내는 함수이다.
먼저 heap 리스트를 초기화 할 때는 각 데이터가 (거리, 레이블값) 형태의 튜플이 되도록 했다. 이렇게 튜플 형태로 데이터를 넣어주면 나중에 힙으로 만들 때 첫 번째 값을 기준으로 정렬되므로 여기에서는 거리를 기준으로 데이터들이 정렬된다.
다음으로 heapq.heapify() 함수를 이용해 heap 리스트가 최소 힙 성질을 만족시키도록 재구조화한다. 이게 뭐 힙이라는 자료형이 따로 있어서 heap이 리스트에서 힙으로 자료형이 바뀌는건 아니다. heap은 여전히 리스트지만 성질만 힙 성질을 만족시키도록 내부 데이터들이 정렬되는 것이다. 이제 heap이 최소 힙 성질을 만족시키도록 정렬되었으므로, heap.heappop() 함수로 데이터를 꺼낼 때 거리가 가장 작은 데이터가 먼저 꺼내진다.
입력 데이터를 모두 힙에 넣었으면 heapq.heappop() 함수로 k개의 데이터를 꺼낸다. 최소 힙의 특성상 거리가 짧은 순으로 3개의 데이터가 차례로 꺼내지며, 이는 힙에 넣어줬을 때처럼 (거리, 레이블값) 형태로 나온다. 따라서 여기에 [1] 인덱싱을 해서 레이블값만 빼오고 이를 knn_label 배열에 저장한다. 이후에는 나이브하게 구현한 것과 똑같은 논리로 진행하면 된다.
이때 시간 복잡도를 한 번 구해보자. $n$개의 데이터가 들어 있는 리스트를 힙으로 재구조화하는데 시간 복잡도는 $O(n)$이며, $n$개의 데이터가 들어있는 힙에서 하나의 데이터를 꺼내는 시간 복잡도는 $O(\log n)$이므로 $k$개의 데이터를 꺼내면 시간 복잡도는 $O(k \log n)$이다. 따라서 총 시간 복잡도는 $O(n) + O(k \log n)$이므로 최소 힙 방식을 사용하면 $O(n)$과 $O(n \log n)$ 사이의 성능을 보인다.
최대 힙 방식을 사용해도 마찬가지이다. 다만 heapq 라이브러리는 기본적으로 최소 힙을 다루므로 최대 힙을 만들고 싶으면 약간의 트릭이 필요하다. 예를 들면, 힙에 데이터를 넣을 때 거리에 -1을 곱해서 (-거리, 레이블값) 형태로 넣는 것이다. 그러면 거리가 가장 먼 데이터가 최소 힙 규칙에 따라 최우선순위가 되므로 데이터를 꺼낼 때 이 데이터가 가장 먼저 나오게 된다. 아까도 말했듯이 최대 힙 방식은 코드만 보이고 넘어갈 것이다.
import heapq
def max_heap_knn(X, y, test_point, k=3):
# 힙으로 사용할 리스트
# 최대 힙으로 구현할 때는 거리에 -1배
# 입력 데이터들을 힙에 넣어준다.
heap = [
(- euclidean_distance(test_point, input_point), input_label[0])
for input_point, input_label in zip(X, y)
]
heapq.heapify(heap) # 최소 힙 성질을 만족하도록 리스트 정렬
# 거리가 가장 먼 n-k개의 데이터를 모두 버리면 거리가 가장 가까운 k개의 데이터만 남는다.
knn_label = np.array([])
for _ in range(len(y)-k):
heapq.heappop(heap) # 그냥 버린다.
knn_label = np.array(heap).T[1].astype(int)
ret = np.bincount(knn_label).argmax()
return ret
③ 코드 실습
로지스틱 회귀에서 사용했던 붓꽃 품종 데이터셋을 이번에도 사용할 것이다. 먼저 다음과 같이 데이터를 불러온다.
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df["target"] = iris.target
df
필자가 고급스러운 시각화는 잘 할 줄 몰라서 외부 코드(https://kirenz.github.io/classification/docs/knn-iris.html)를 약간 변형했다. 코드를 다음과 같이 작성했다.
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
X = df[["petal length (cm)", "petal width (cm)"]]
y = df[["target"]]
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
def plot_iris_knn():
x_min, x_max = X["petal length (cm)"].min() - .1, X["petal length (cm)"].max() + .1
y_min, y_max = X["petal width (cm)"].min() - .1, X["petal width (cm)"].max() + .1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plot also the training points
plt.scatter(X["petal length (cm)"], X["petal width (cm)"], c=y["target"], cmap=cmap_bold)
plt.xlabel('petal length (cm)')
plt.ylabel('petal width (cm)')
plt.axis('tight')
plot_iris_knn()
실행 결과
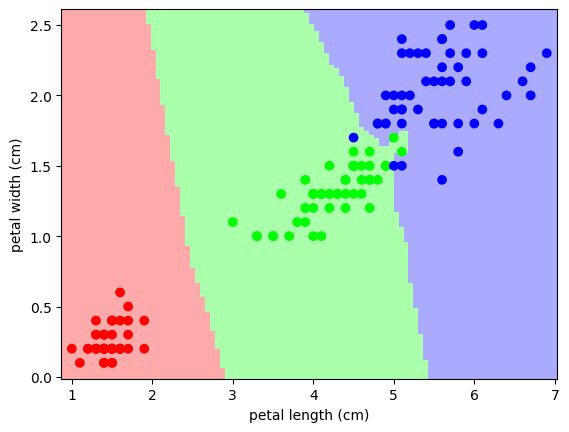
빨간색이 setosa, 초록색이 versicolor, 파란색이 virginica이다.
꽃잎(petal)의 길이를 x축, 너비를 y축으로 두고 각 데이터를 산점도로 나타냈을 때, 품종별로 구분이 꽤 잘 되는 것을 확인할 수 있다. 실제로 예측을 수행하면 꽤 준수한 정확도를 보인다.
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42, stratify=y
)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
print("accuracy:",accuracy_score(y_test, y_pred))accuracy: 0.9333333333333333
꽃잎이 아니라 꽃받침(sepal)에 대해서 그래프로 나타낸 것은 어떨까?
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
X = df[["sepal length (cm)", "sepal width (cm)"]]
y = df[["target"]]
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
def plot_iris_knn():
x_min, x_max = X["sepal length (cm)"].min() - .1, X["sepal length (cm)"].max() + .1
y_min, y_max = X["sepal width (cm)"].min() - .1, X["sepal width (cm)"].max() + .1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# Plot also the training points
plt.scatter(X["sepal length (cm)"], X["sepal width (cm)"], c=y["target"], cmap=cmap_bold)
plt.xlabel('sepal length (cm)')
plt.ylabel('sepal width (cm)')
plt.axis('tight')
plot_iris_knn()
이전 코드에서 'petal'만 모두 'sepal'로 바꿔주면 된다.
실행 결과
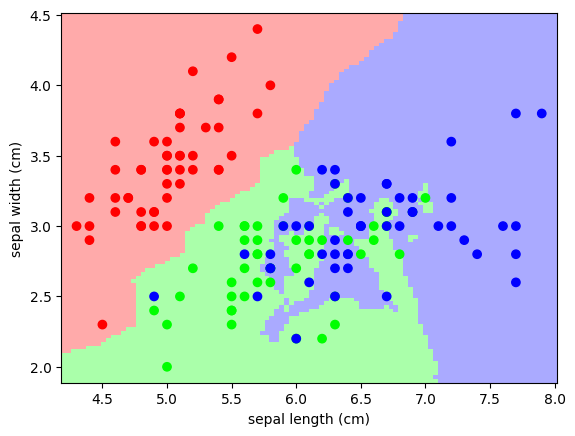
빨간색(setosa)는 구분이 잘 되는 편인데, 초록색(versicolor)과 파란색(virginica)은 뭔가 뒤섞인 느낌이다. 이러면 꽃잎의 길이와 너비를 피처로 사용한 것에 비해 정확도가 확실히 떨어질 것 같은 느낌이 든다.
실제로 예측을 수행하면 정확도가 좀 낮게 나온다. (모델 예측시키고 정확도 구하는 코드는 아까와 같음)
accuracy: 0.6666666666666666
그런데 어느 부분에서 많이 틀렸을까? setosa를 잘못 예측한 경우는 거의 없을 것 같다. 위 그림에서 그나마 맨 아래 위치한 빨간 점 하나가 헷갈릴만 한데 그걸 제외하면 틀릴만한 데이터는 거의 없다. 하지만 초록 점과 파란 점은 매우 뒤섞여 있는 편이라, versicolor를 virginica로 잘못 예측했거나 virginica를 versicolor를 잘못 예측한 경우가 대부분일 것 같다.
우리는 이를 혼동 행렬(confusion matrix)과 히트맵(heatmap)으로 나타낼 수 있다. 혼동 행렬은 실제로 setosa인 붓꽃을 setosa로 맞게 예측한 개수, 또는 versicolor이나 virginica로 잘못 예측한 개수를 나타내주는 행렬인데, 일종의 정오표라고 생각하면 된다. 그리고 이 혼동 행렬을 시각화 해주는 것이 히트맵이다. 텍스트로만 봐서는 이해가 잘 안되니 다음 코드를 실행시키고 결과를 보자.
import seaborn as sns
from sklearn.metrics import confusion_matrix
# 혼동 행렬 계산
cm = confusion_matrix(y_test["target"], y_pred)
# 히트맵 시각화
plt.figure(figsize=(6, 5))
sns.heatmap(cm, annot=True, cmap="Blues", fmt="d", xticklabels=["setosa", "versicolor", "virginica"], yticklabels=["setosa", "versicolor", "virginica"])
plt.xlabel("Predicted")
plt.ylabel("True")
plt.title("Prediction Result Confusion Matrix")
plt.show()
출력 결과
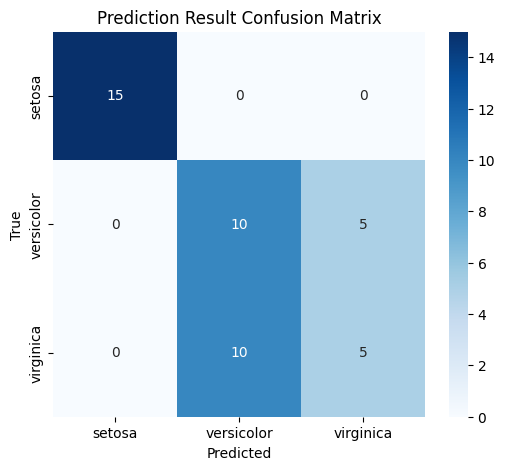
먼저 앞에서 예상한대로 setosa에 대해서는 예측이 완벽하다. setosa인 것을 다른 품종으로 예측한 것도 없고, 반대로 setosa가 아닌 것을 setosa로 예측한 경우도 없다.
하지만 versicolor와 virginica에 대해서는 틀린 예측이 많다. 15개의 versicolor 중에 5개를 virginica로 잘못 예측했으며, 심지어 15개의 virginica 중에서는 절반 이상인 10개를 versicolor로 잘못 예측했다(보기 헷갈리면 위 히트맵에서 대각 성분이 옳게 예측한 것이라고 생각하면 된다). 그림으로 확인했을때도 versicolor와 virginica는 뭔가 뒤죽박죽 섞여있는 느낌이었는데, 이러한 데이터 분포로 인해 kNN의 정확도가 확연히 떨어진 것을 확인할 수 있었다.
정리하자면 꽃잎의 길이와 너비를 피처로 사용했을 때는 각 품종의 영역이 명확하게 구분되어 있어서 kNN으로 분류하기가 쉬웠다. 그래서 예측 정확도도 90% 이상으로 매우 높게 나타났다. 하지만 꽃받침의 길이와 너비를 피처로 사용했을 때는 두 품종이 뒤섞여 있어서 kNN으로 분류하기가 어려웠고, 이로 인해 정확도가 60%대까지 떨어졌음을 알 수 있었다.
'머신러닝, 딥러닝 개념 > 지도 학습' 카테고리의 다른 글
| 지도 학습(6+) : 서포트 벡터 머신 심화 (1) | 2025.03.15 |
|---|---|
| 지도 학습(6) : 서포트 벡터 머신 (1) | 2025.03.14 |
| 지도 학습(4) : 로지스틱 회귀 (3) | 2025.03.10 |
| 지도 학습(3) : 다항 회귀, 릿지 회귀, 라쏘 회귀, 엘라스틱 넷 (1) | 2025.03.05 |
| 지도 학습(2) : 다중 선형 회귀 (1) | 2025.03.01 |