2025. 2. 26. 11:25ㆍ머신러닝, 딥러닝 개념

① 머신러닝 알고리즘
- 지도 학습(Supervised Learning) : 라벨(정답)이 있는 데이터를 입력으로 받아 학습하는 알고리즘. 대표적으로 회귀와 분류가 있다.
- 비지도 학습(Unsupervised Learning) : 라벨이 없는 데이터를 입력으로 받아 그 패턴을 학습하는 알고리즘. 대표적으로 클러스터링이 있다.
- 회귀(Regression) : 지도 학습의 일종으로, 하나의 종속변수와 하나 이상의 독립변수 사이의 관계를 추정하는 작업
- 분류(Classification) : 지도 학습의 일종으로, 데이터를 사전에 정의된 클래스 혹은 항목에 할당하는 작업
- 클러스터링(Clustering) : 비지도 학습의 일종으로, 유사성이 높은 데이터들을 같은 그룹으로 묶는 작업이다.
머신러닝 알고리즘 중 가장 기본적이고 쉬운 것을 꼽으라고 하면 단연 선형 회귀(Linear Regression)다. 이 선형 회귀라는 애는 고등 수학으로 따지면 다항식 같은 부분이요, 한국사로 따지면 선사시대 같은 부분이다. 한국사능력검정시험 강의 들을때 최태성 선생님이 구석기 신석기만큼은 선생님보다 학생들이 더 빠삭하게 알고 있을거라고 하셨는데 머신러닝에서는 선형 회귀가 딱 그런 포지션이 아닐까 싶다. 여기서도 개론이니만큼 선형 회귀를 예로 들어보려고 한다. 데이터가 다음과 같이 주어져 있다고 하자.

그러면 선형 회귀 알고리즘은 이 데이터들의 특징을 가장 잘 대표하는 직선 하나를 다음과 같이 뽑아낸다.

당연히 이 네 점을 모두 지날 수 있는 직선은 없다. 심지어는 네 점 중 단 하나도 안 지나도 된다. 그저 네 점을 가장 잘 대표하는 직선을 찾아주면 된다.
② 손실 함수
그런데 직선이 데이터를 잘 대표한다? 이 말은 좀 추상적이고 와닿지 않을 수도 있다. 과연 어떤 직선이 주어진 데이터들을 잘 대표하는 직선일까? 이를 평가하는 지표가 '손실 함수(Loss Function)'가 되겠다. 또는 비용 함수(Cost Function)라고 하기도 한다.
손실 함수란, 머신러닝 혹은 딥러닝 모델의 출력값과 사용자가 원하는 출력값의 오차로 정의된다. 즉, 손실 함수 값이 최소가 된다면 학습이 잘 된 것이라고 할 수 있다. 따라서 주어진 데이터들을 잘 대표하는 직선을 찾는다는 것은 주어진 데이터들에 대해 손실 함수 값이 가장 작은 직선을 찾는 것과 같은 의미라고 보면 된다.
손실 함수의 종류는 여러가지가 있는데, 선형 회귀에서는 보통 평균 제곱 오차(Mean Squared Error, MSE)를 사용한다.

평균 제곱 오차의 정의는 간단하다. 각 데이터에 대한 오차 제곱의 평균이 평균 제곱 오차가 된다. 실제값($Y_i$)과 예측값($\hat{Y_i}$)의 차이가 오차가 될텐데, 이 오차를 모든 데이터에 대해 구한 다음에 각각을 제곱한다. 그런 다음 데이터의 개수($n$)로 나눠주면 된다.
따라서 선형 회귀 알고리즘에서 손실 함수를 MSE로 사용한다는 것은, 주어진 데이터에 대한 MSE 값이 가장 작은 직선을 찾는 것을 목표로 하는 것이라고 할 수 있다.
③ 최적화
그렇다면 손실 함수 값이 가장 작은 직선을 어떻게 찾을까? 예를 들어, 다음 그림에서 우리는 $y=x+3$이 가장 MSE가 작은 직선이라는 것을 직관적으로 알 수 있긴 하지만 컴퓨터는 이를 어떻게 찾을까? 이 고민에 대한 해결 방법을 제공하는 방법론이 '최적화(Optimization)'가 되겠다.

최적화는 쉽게 말해서 오차 함수를 최소화하는 파라미터값을 찾는 과정이라고 생각하면 된다. 선형 회귀에는 어떤 파라미터가 있을까? 직선은 중고등학교 방식으로 $y=ax+b$로 표현할 수 있기 때문에, 여기에 존재하는 파라미터는 기울기($a$)라는 파라미터와 y절편($b$)이라는 파라미터가 있다. 하지만 머신러닝에서는 보통 기울기 대신 가중치라는 용어를 쓰며, 기호도 $a$가 아니라 가중치 Weight의 앞글자를 따서 $W$로 쓴다. 그리고 y절편 대신 편향이라는 용어를 쓰는데, 기호는 우연히도 편향을 뜻하는 영단어 bias의 앞글자가 b라서 똑같이 $b$로 쓴다. 따라서 머신러닝에서 선형 회귀 식은 $y=Wx+b$라고 쓰는 것이 일반적이다.
따라서 선형 회귀 알고리즘에서 오차 함수를 MSE로 할 때, 최적화 알고리즘의 목표는 MSE 값을 최소로 하는 선형 회귀식의 가중치 및 편향(파라미터)을 찾는 것이다.
가장 직관적이고 쉬운 최적화 알고리즘으로 경사 하강법(Gradient Descent)이 있다. 경사 하강법은 말 그대로 경사를 타고 아래로 내려가는 느낌이라 경사 하강법이라고 하는데, 다음 예시를 보면 이해가 더 쉬울 것 같다.
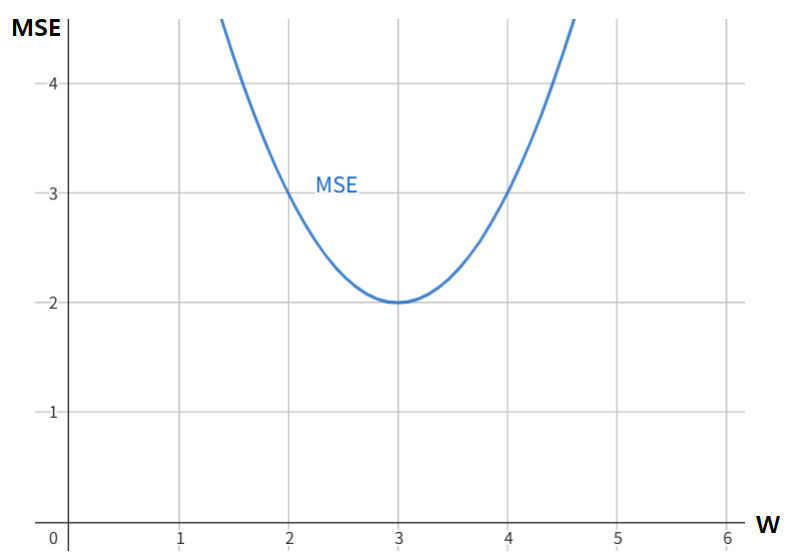
위 그래프에서 보는 것처럼 선형 회귀식에서 MSE는 가중치($W$)에 대해 이차함수 꼴이다. 사실 아까 보여준 수식 $\displaystyle {\rm MSE} = \frac{1}{n} \sum_{i=1}^n \left( Y_i - \hat{Y_i} \right)^2$에 $\hat{Y_i} = Wx + b$를 집어 넣어보면 당연하게 알 수 있는 사실이다. 물론 가중치에 대해서 뿐만 아니라 편향($b$)에 대해서도 이차함수이다.
그림을 보다시피 MSE가 최소가 되는 가중치는 3으로 되어 있는데, 컴퓨터에는 현재 가중치가 4로 설정된 상태라고 하자.

오차를 줄이려면 가중치를 어떻게 변경시켜야 할까? 물론 우리는 그래프를 보면 가중치가 3이 되어야 오차가 최소가 된다는 것을 알 수 있다. 하지만 컴퓨터 입장에서는 이런 그래프 따위는 주어지지 않는다. 따라서 W를 줄여야 한다는 판단을 하도록 유도하려면 다른 판단 지표가 필요하다. 컴퓨터가 현재 위치에서 알 수 있는 지표는 다음과 같이 크게 두 가지가 있다.

현 위치에서 MSE 값과 MSE 그래프의 기울기(미분계수)를 컴퓨터가 계산할 수 있는데, 이 기울기가 엄청난 힌트가 된다.
기울기가 2라고 되어있는데, 기울기가 2이면 $W$ 값을 크게 해야 할까 작게 해야 할까? 고등 수학을 공부했다면 미분계수가 양수이면 함수는 그 점에서 우상향한다는 것을 당연히 알고 있을 것이다. 따라서 현재 위치는 MSE가 우상향하고 있는 위치이다. 우리는 MSE를 최소화하는게 목표라고 했는데, 현재 위치는 MSE가 우상향하고 있는 위치니까 MSE를 떨어뜨리려면 $W$가 왼쪽으로 가야한다는 것을 알 수 있겠지. 그러니까 여기서 $W$는 작아져야 한다.
하나만 더 해보자. 이번에는 현재 위치가 다음과 같이 $W=2$로 되어 있다.
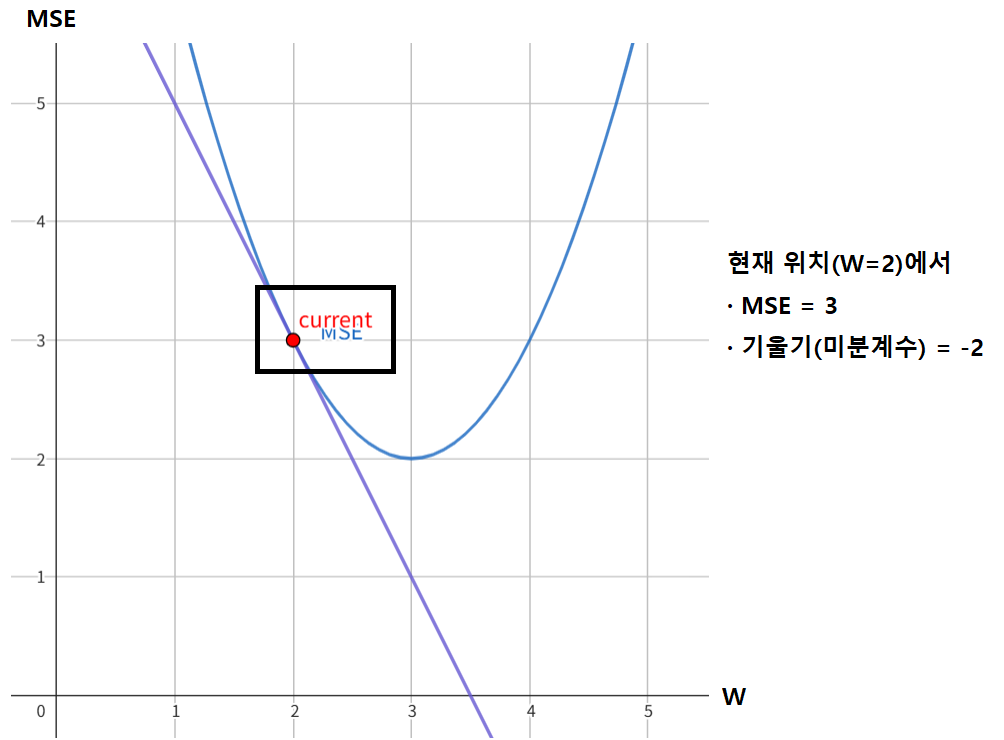
이번에는 기울기가 음수로 나왔다. 기울기가 음수면 함수는 그 점에서 우하향한다. 그러면 MSE를 줄이려면 $W$가 오른쪽으로 가야, 즉 $W$가 커져야 한다는 것을 알 수 있을 것이다.
물론 양수 음수인지 뿐만 아니라 기울기 숫자 자체도 중요하다. 기울기가 10이라면 기울기가 2일 때보다 더 많이 왼쪽으로 이동해야 하고, 기울기가 0.5라면 기울기가 2일 때보다 더 작은 폭으로 왼쪽으로 이동해야 한다.
④ 활성화 함수
활성화 함수(Activation Function)는 사실 여기서 설명하기엔 어려운 개념이긴 하다. 활성화 함수에 대해 설명하려면 인공 신경망이라는 개념에 대한 언급이 선행되어야 하기 때문이다. 따라서 활성화 함수에 대한 설명은 보류하고 나중에 따로 포스팅할 기회가 있다면 그 때 하기로 하자. 활성화 함수의 대표적인 예로 ReLU, tanh, sigmoid, softmax 등이 있다.